このページは、中学1年生で習う「角すいや円すいの体積」が学習できるページです。
この問題のポイント
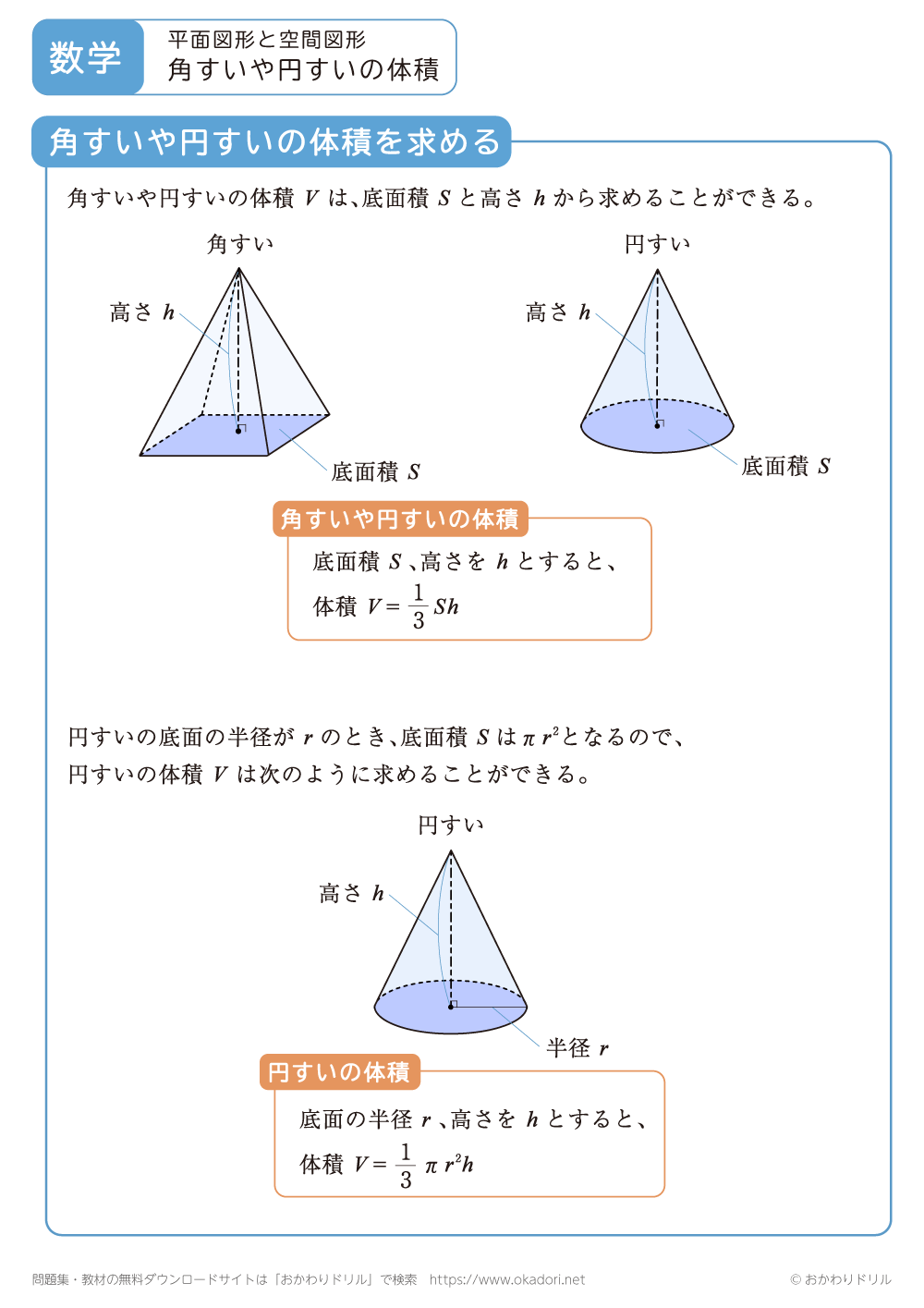
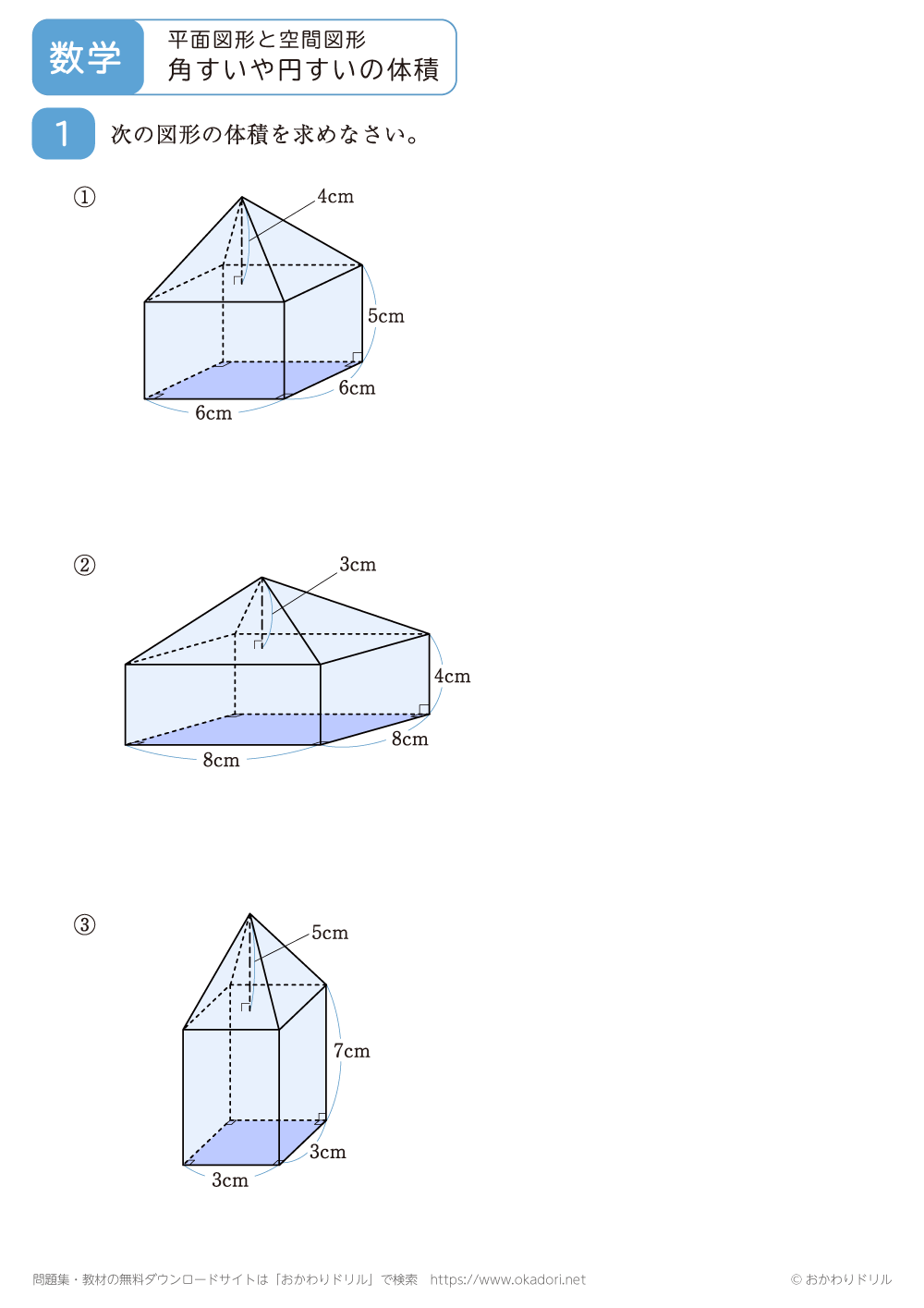
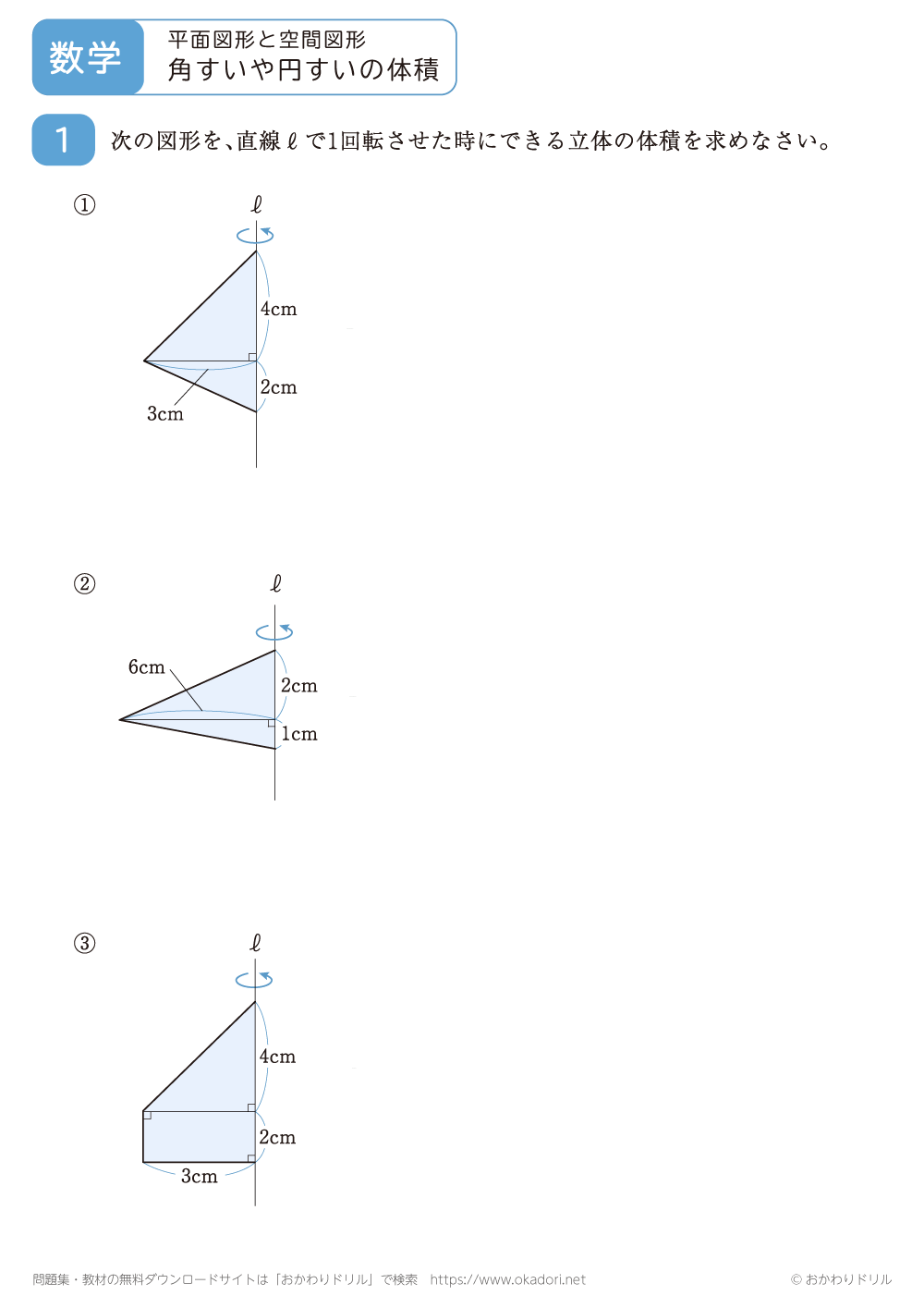
・角すいや円すいの体積Vは、底面積Sと高さhから求めることができます。
V=1/3×Sh
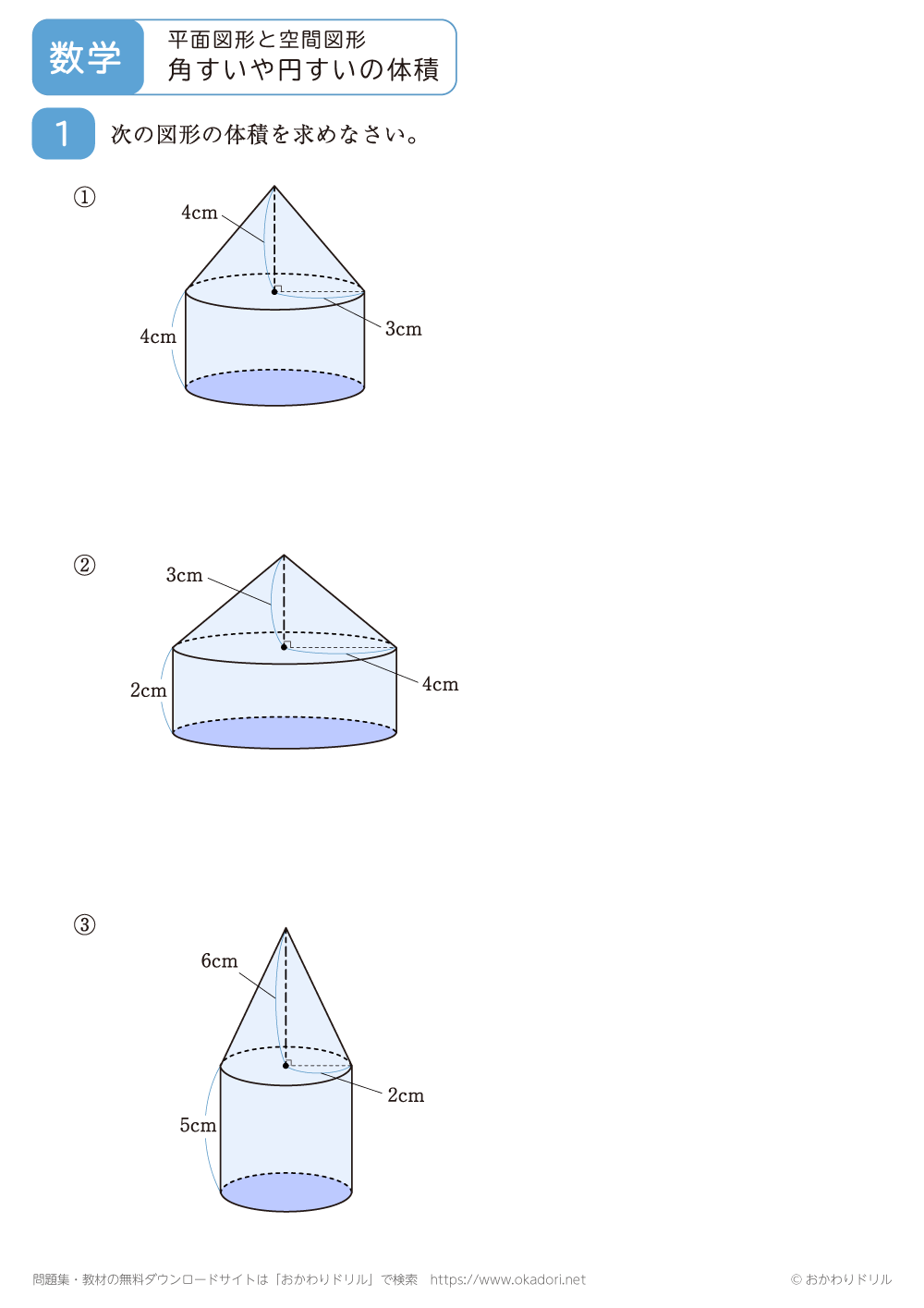
・円すいの底面の半径がrのとき、底面積Sはπr2となるので、体積Vは次のようになります。
V=1/3×πr2h

ぴよ校長
角すいや円すいの体積を求める問題を解いてみよう!
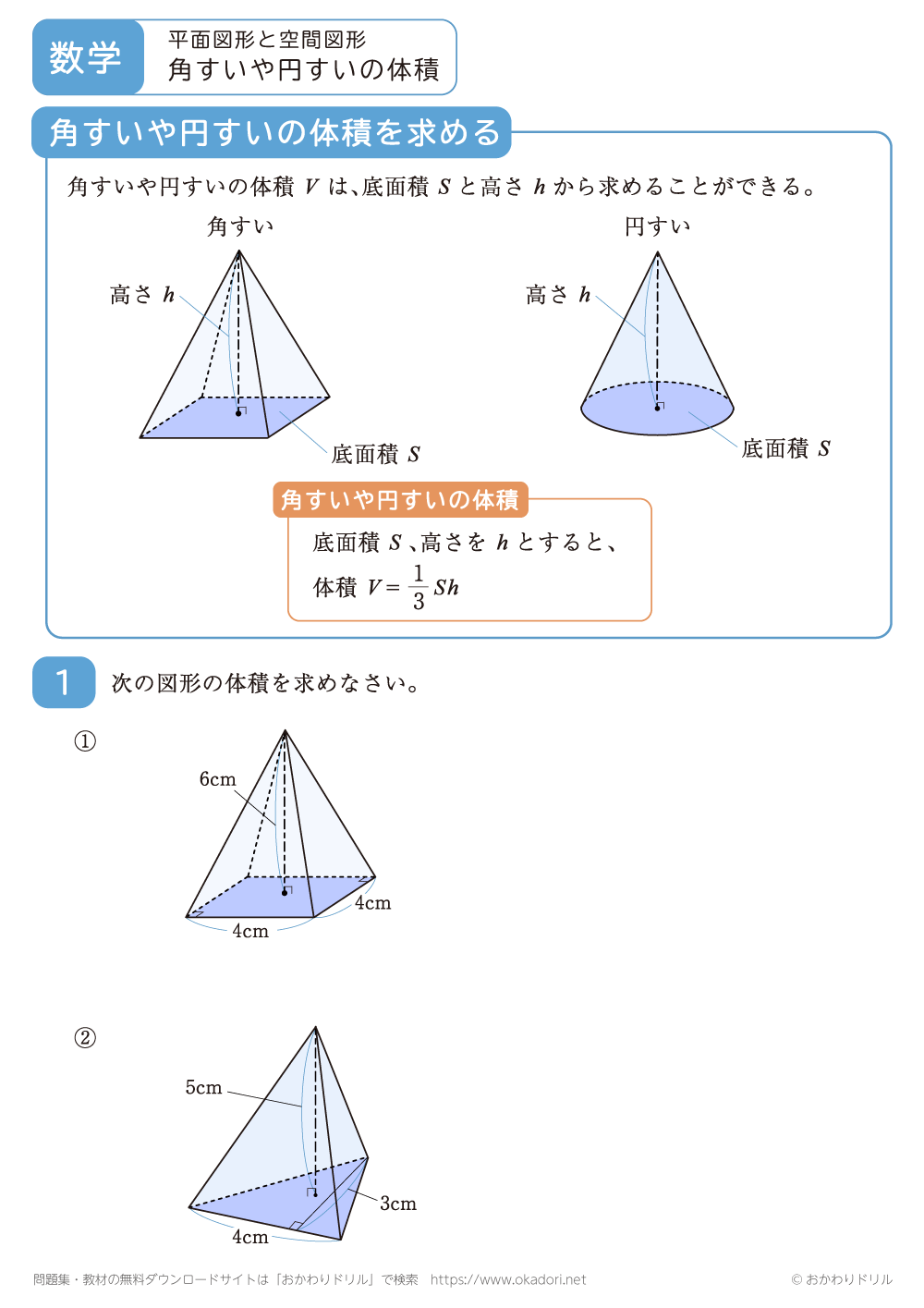
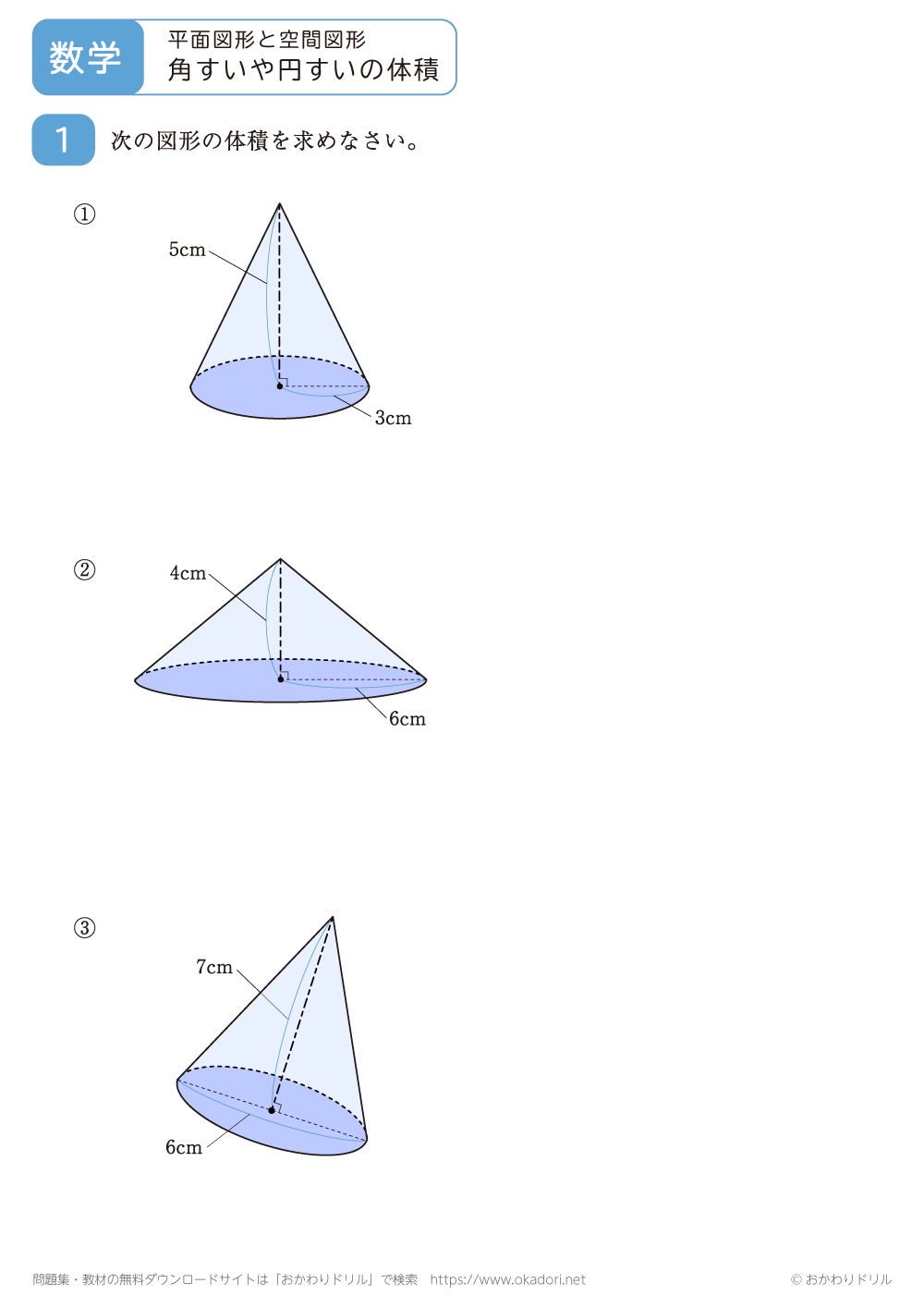
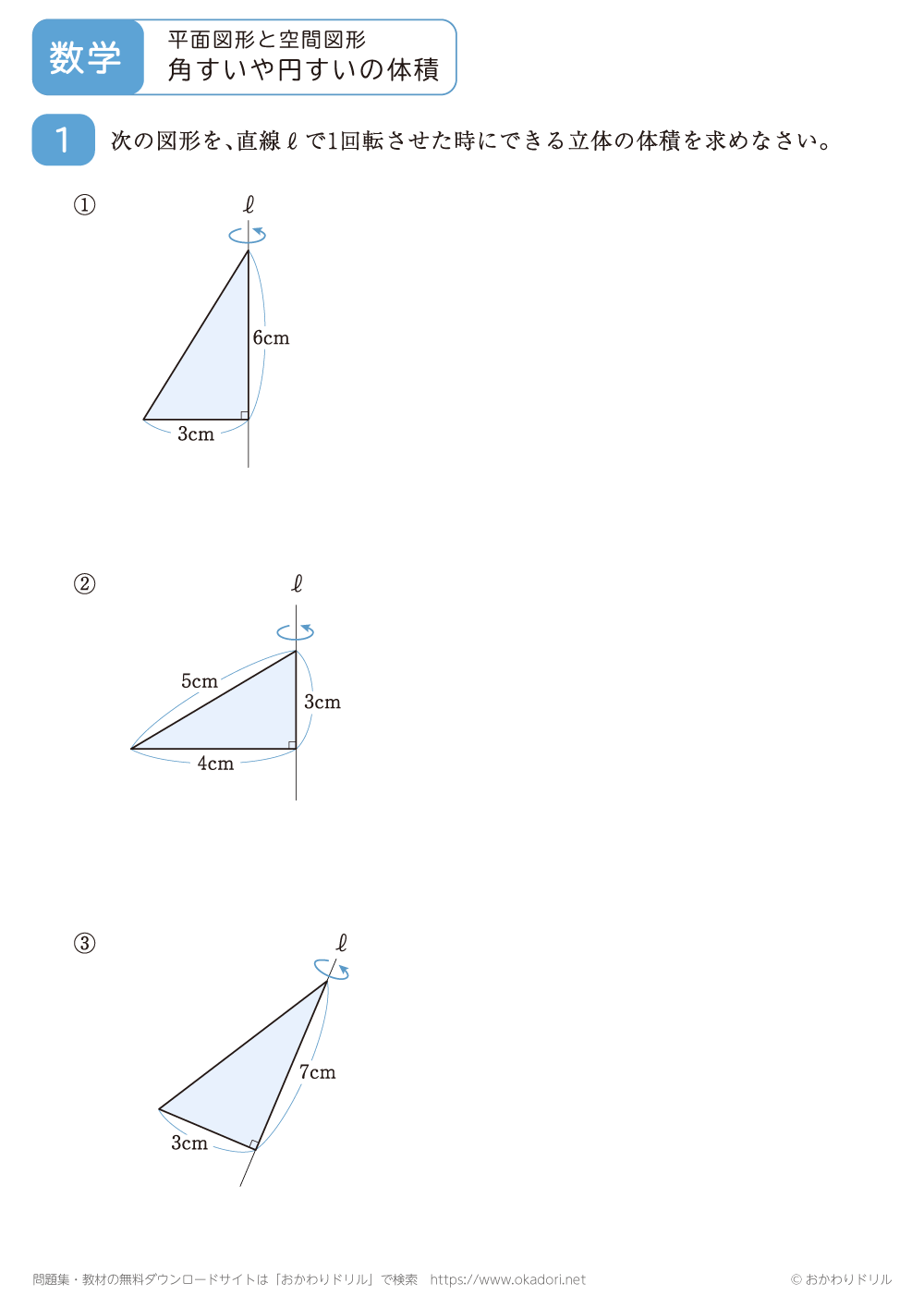
角すいや円すいの体積を求める問題です。角すいや円すいの体積は、1/3×底面積×高さで求めることができます。

ぴよ校長
それでは、さっそく問題を解いてみよう!
「角すいや円すいの体積」の学習プリントはこちら
下の画像やリンク文字をクリックするとのPDFファイルが開きます。ダウンロード・印刷してご利用ください。
解説テキスト
問題プリント
「平面図形と空間図形」の問題プリント一覧
- 垂直二等分線や垂線のかき方
- 角の二等分線のかき方
- 正多面体の頂点と辺の数
- 角柱・円柱:①角柱や円柱の体積、②角柱や円柱の表面積
- おうぎ形:①孤の長さ、②面積と中心角、③面積と孤の長さ
- 角すい・円すい:①角すいや円すいの体積、②角すいや円すいの表面積、
- 球:①球の表面積、②球の体積
- 鉛筆の芯の体積