 ここでは、直角三角形の合同条件について、確認したいと思います。
ここでは、直角三角形の合同条件について、確認したいと思います。
直角三角形の合同条件は、普通の三角形の合同条件とは少し違う内容になっています。中学生の図形問題を解くためにも、直角三角形の合同条件をぜひ覚えておきましょう。
この公式のポイント
・直角三角形の合同条件
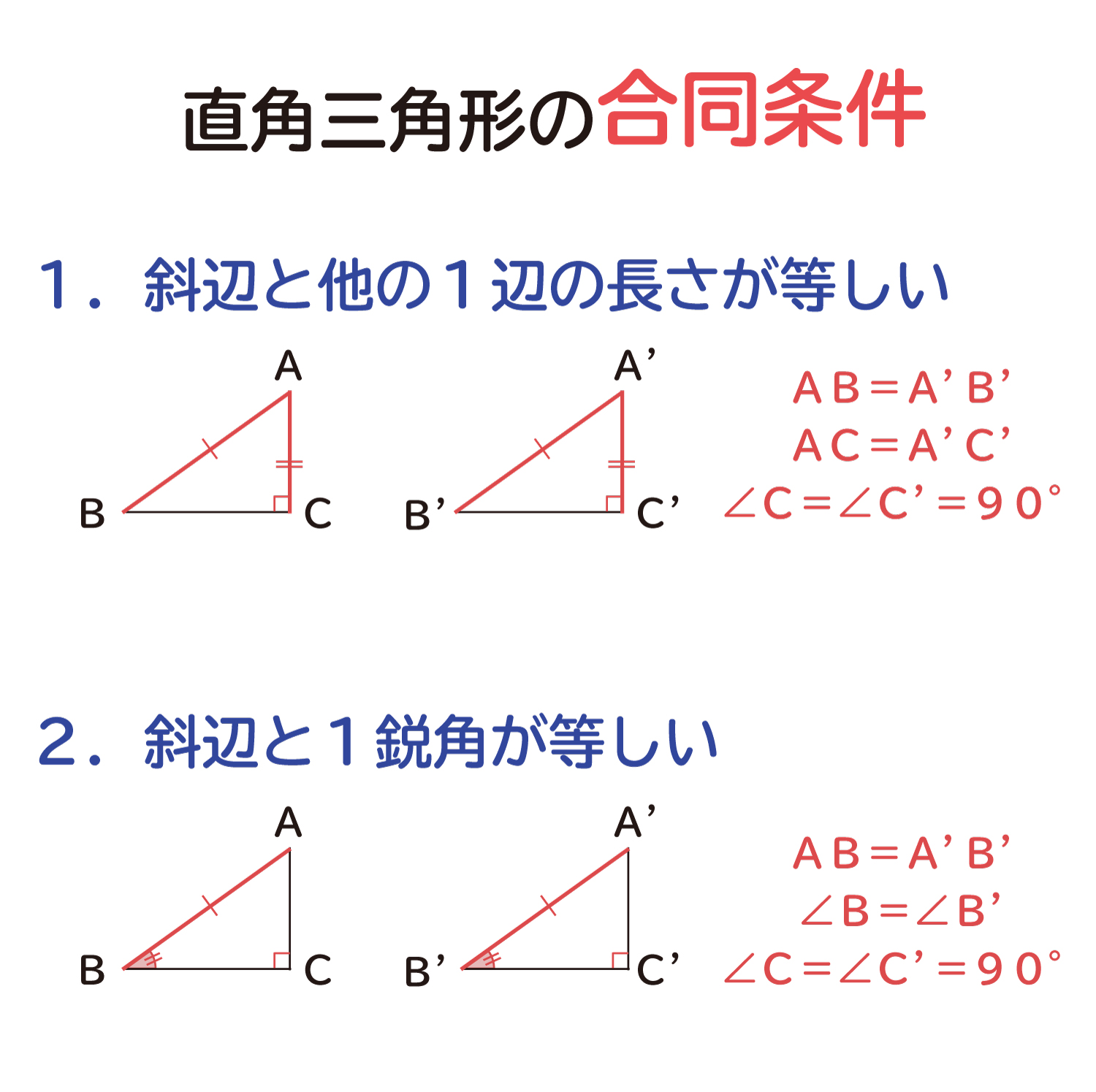
1.斜辺と他の1辺の長さが等しい
2.斜辺と1鋭角が等しい
上の2つの合同条件のうちの、どれか1つが当てはまれば、合同な直角三角形と言うことが出来ます。

参考:普通の三角形の合同条件については、下のリンクを参考にしてみて下さい。
-
-
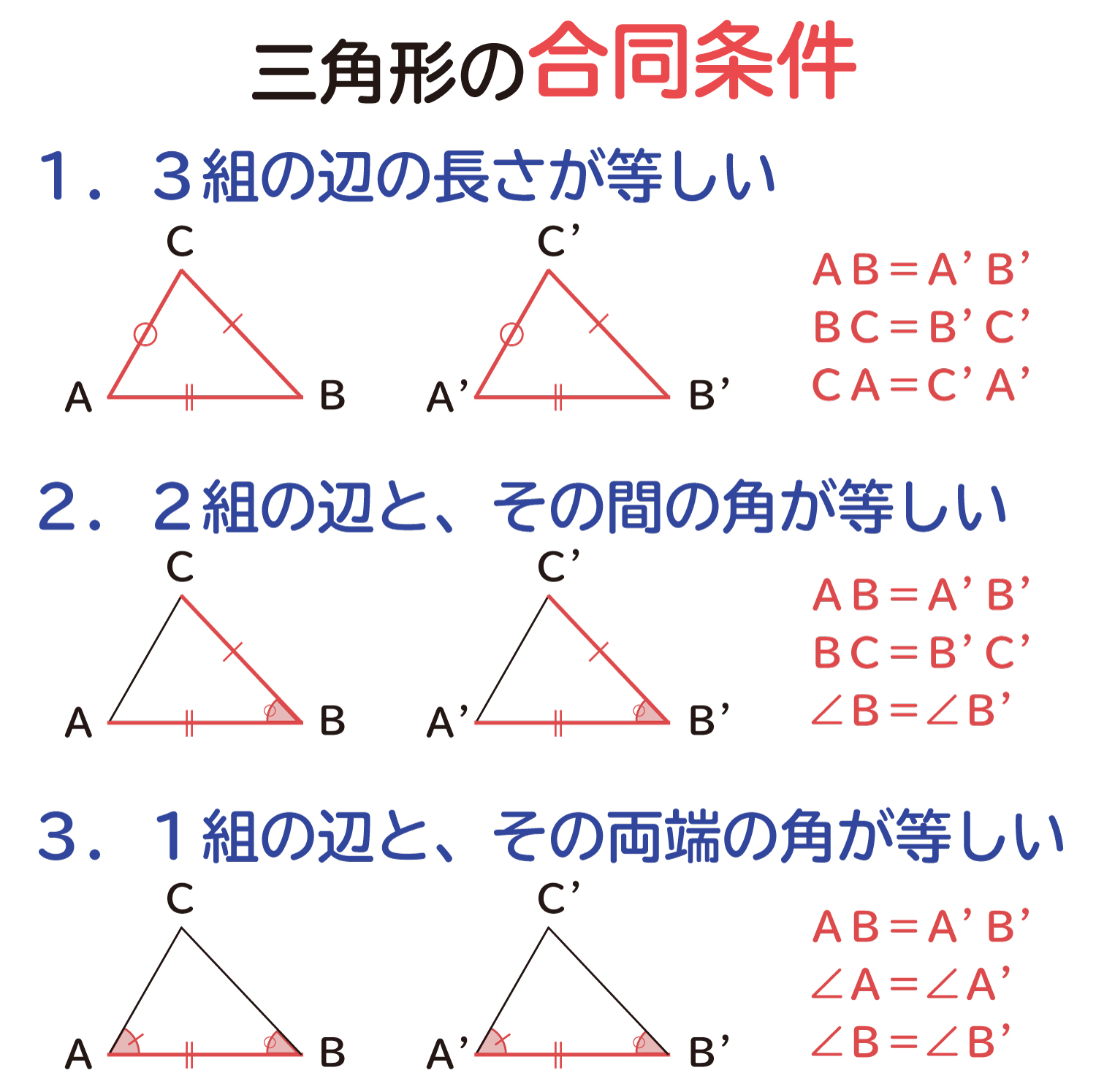
三角形の合同条件の説明
ここでは、三角形の合同条件について、確認したいと思います。 中学校では、三角形の合同を使った様々な図形問題が出てきます。図形問題を解くために ...
続きを見る
直角三角形の合同条件は、普通の三角形の合同条件とは違うので、注意してください。斜辺が分かれば、他の1辺か、1鋭角のどちらかが分かれば良いということになります。

「直角三角形の合同条件」の確認
最初に、直角三角形の合同条件の1つ目「斜辺と他の1辺の長さが等しい」を確認していきます。
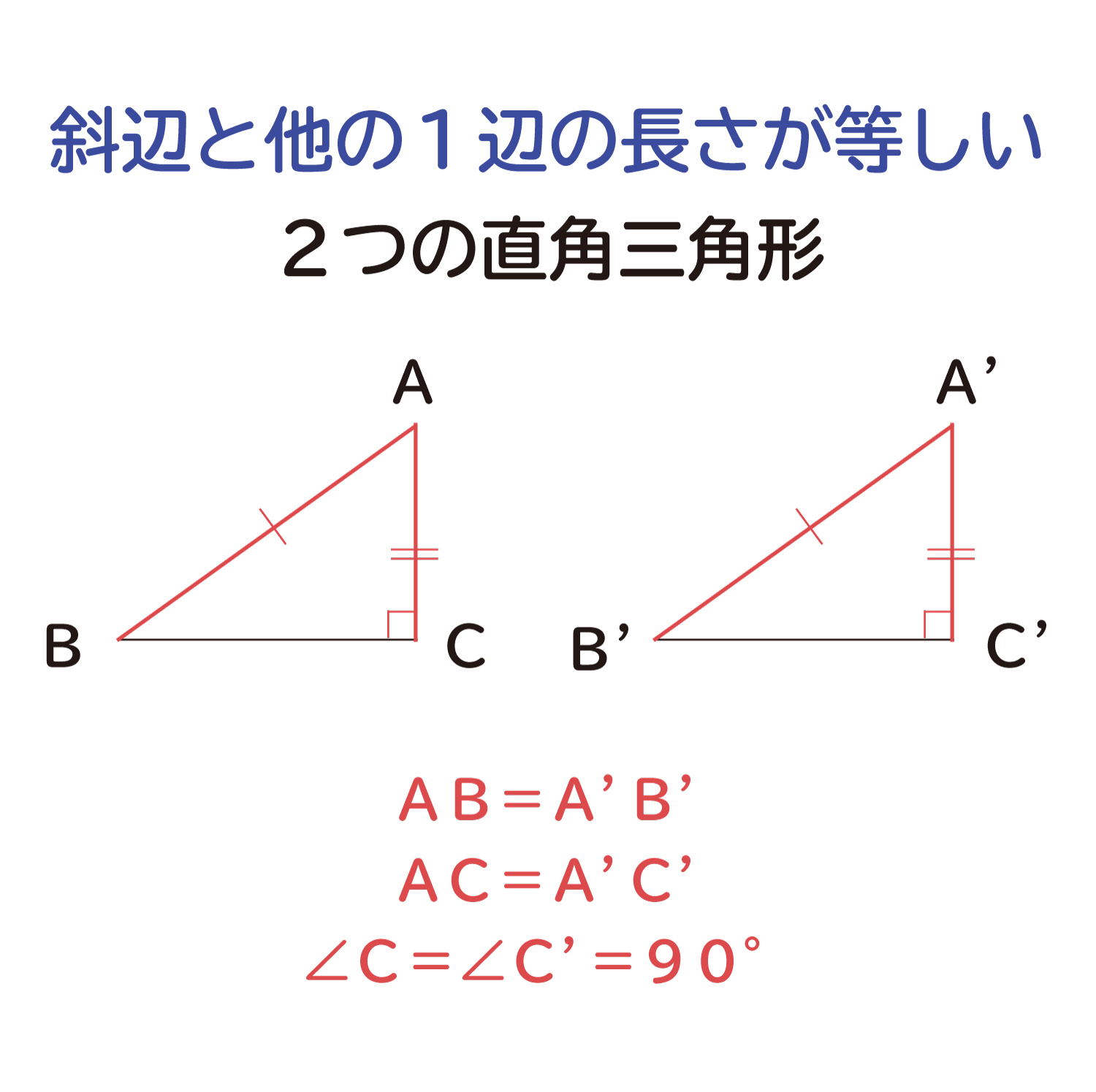
まず、下の図のように「斜辺と他の1辺が等しい」2つの直角三角形を考えます。
AB=A’B’、AC=A’C’、∠C=∠C’=90°
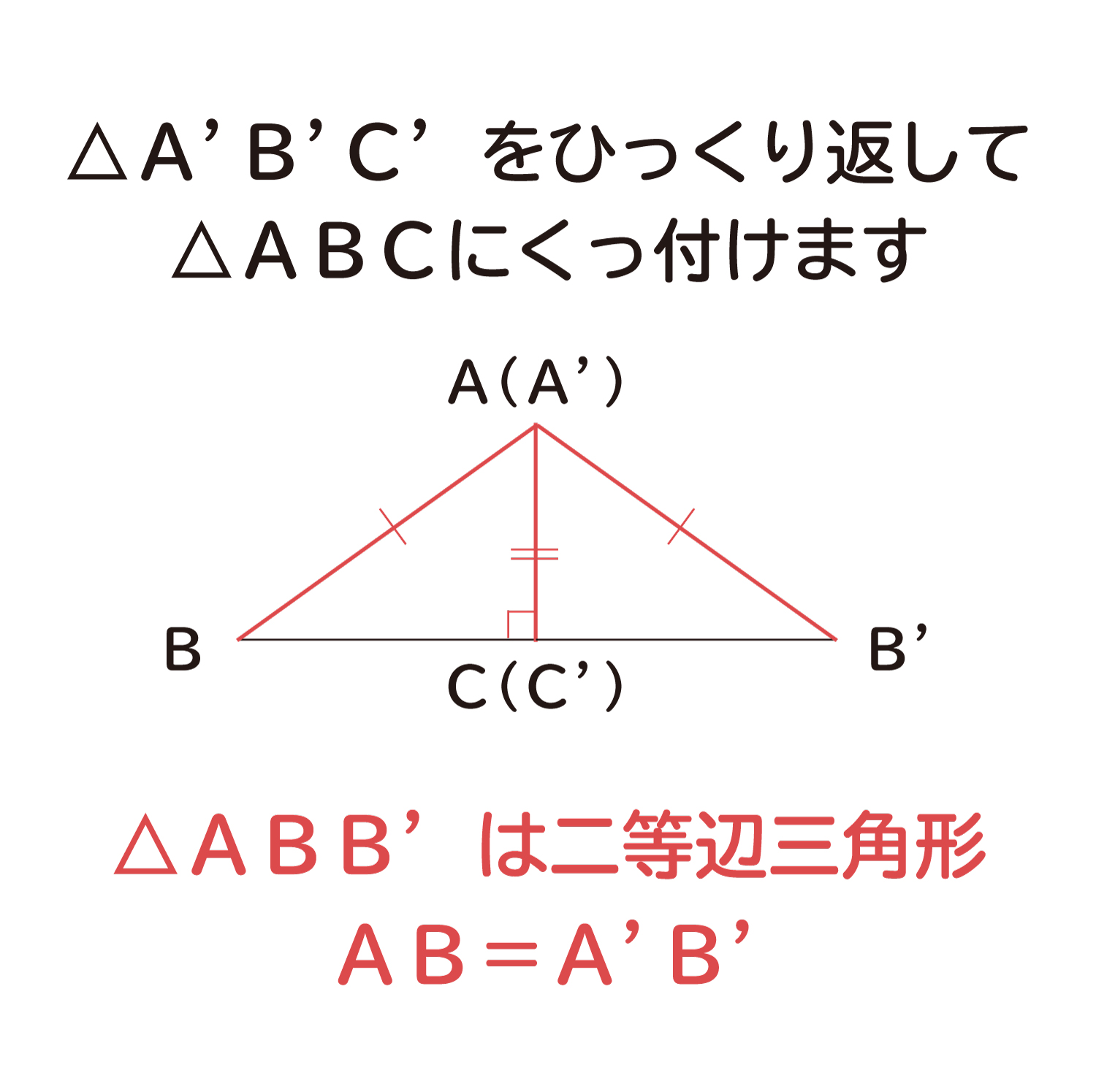
ここで、下の図のように△A’B’C’をひっくり返して△ABCにくっ付けます。すると、△ABB’は2辺が等しい(AB=A’B’)二等辺三角形になっています。
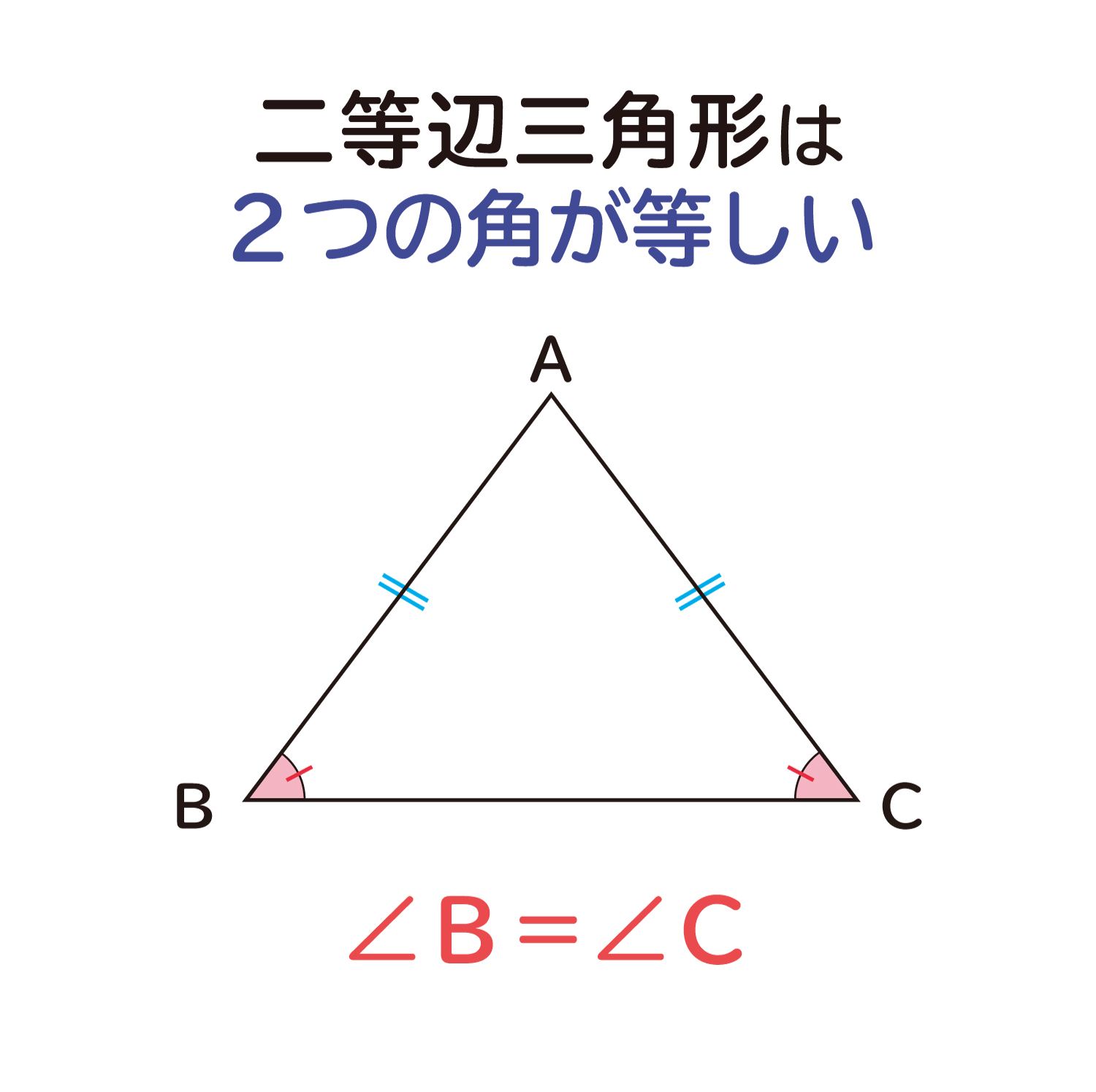
二等辺三角形は、2つの角が等しくなる性質があるので、∠B=∠B’になると言うことが出来ます。
参考:二等辺三角形の2つの角が等しくなる理由については、下のリンクを参考にしてみて下さい。
-
-
”二等辺三角形の2つの角は等しくなる”ことの説明
二等辺三角形は、「2つの辺の長さが等しい三角形」と定義されます。 二等辺三角形は2つの辺の長さが等しいことでさまざまな性質が現れてきます。そ ...
続きを見る
ここで、三角形の内角の和は180°なので、
△ABCにおいて、∠BAC=180°-∠B-90°
△AB’Cにおいて、∠B’AC=180°-∠B’-90°
となり、∠B=∠B’なので、∠BAC=∠B’ACと言えます。
以上のことから、△ABCと△AB’Cは、1辺(AB=AB’)とその両端の角が等しい合同な三角形となります。

次に、合同条件の2つ目「斜辺と1鋭角が等しい」を確認していきます。
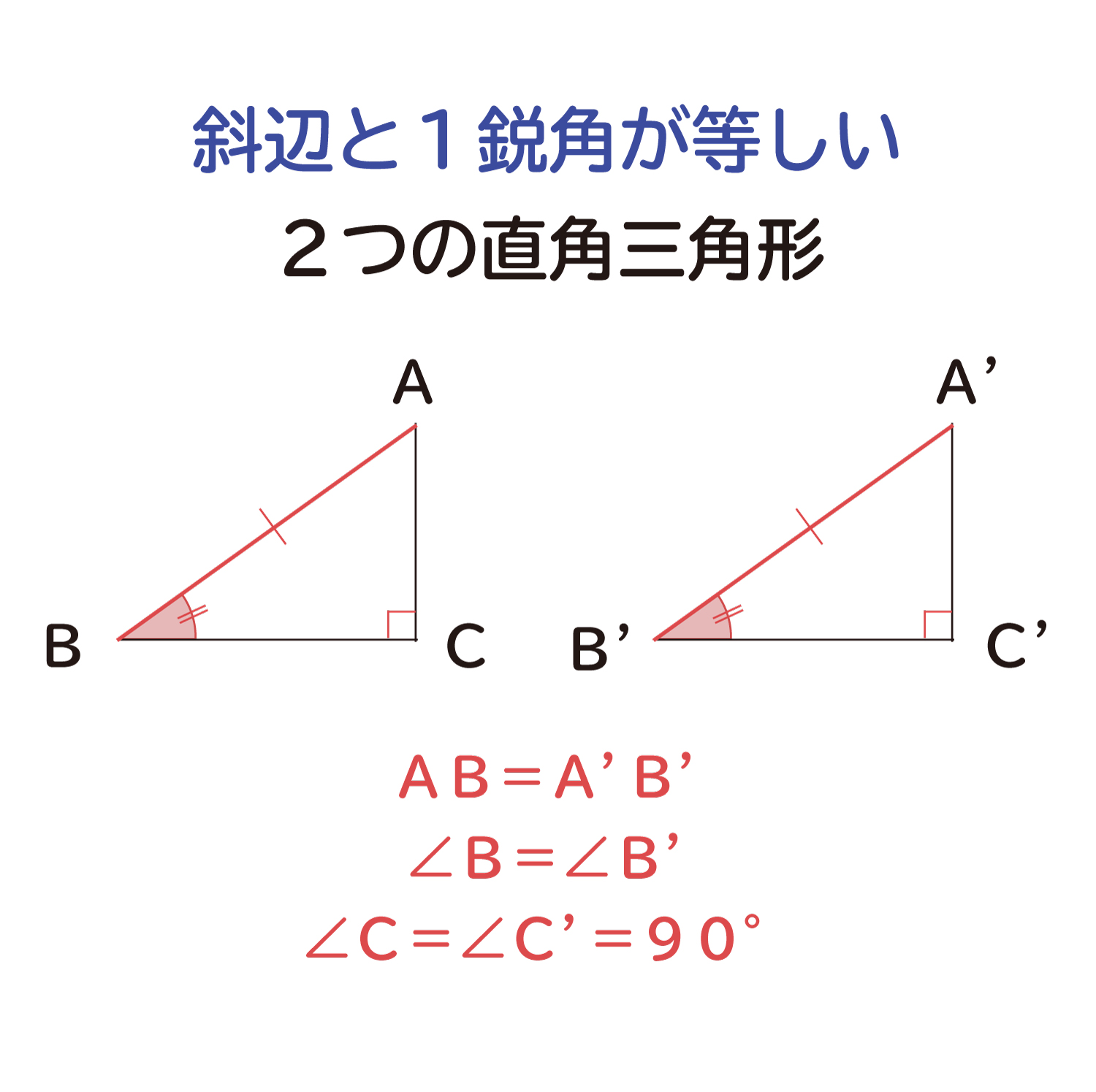
下の図のように「斜辺と1鋭角が等しい」2つの直角三角形を考えます。
AB=A’B’、∠B=∠B’、∠C=∠C’=90°
これは先ほどと同じ三角形の内角の和は180°の公式を使うと、
△ABCにおいて、∠BAC=180°-∠B-90°
△A’B’C’において、∠B’A’C’=180°-∠B’-90°
となり、∠B=∠B’なので、∠BAC=∠B’A’C’と言えます。
△ABCと△A’B’C’は、1辺(AB=A’B’)とその両端の角が等しい合同な三角形となります。

まとめ
・直角三角形の合同条件には下の2つがあります。
1.斜辺と他の1辺の長さが等しい
2.斜辺と1鋭角が等しい

「中学2年生の公式の解説」一覧
- 連立方程式の解き方の説明ー代入法を使った解き方ー
- 連立方程式の解き方の説明ー加減法を使った解き方ー
- 直線が交わるときにできる対頂角の性質
- 平行線の同位角と錯角の性質
- 「三角形の1つの外角は、それと隣り合わない2つの内角の和に等しい」ことの説明
- 「n角形の内角の和は、" 180°×(n-2)”」になる説明
- 「n角形の外角の和は 360° 」になる説明
- 三角形の合同条件の説明
- ”二等辺三角形の2つの角は等しくなる”ことの説明
- ”二等辺三角形の頂角の二等分線は、底辺を垂直に二等分する”ことの説明
- ”2つの角が等しい三角形は、二等辺三角形になる”ことの説明
- 直角三角形の合同条件の説明
- ”平行四辺形の対辺の長さは等しくなる”ことの説明
- ”平行四辺形の対角の角度は等しくなる”ことの説明
- ”平行四辺形の対角線は中点で交わる”ことの説明
