ここでは中学生の数学で出てくる、２本の直線が交わったときにできる対頂角（たいちょうかく）の性質について確認しておきたいと思います。
この公式のポイント
・直線が交わるとき、交点で互いに向かい合った角を対頂角と言います。
・対頂角の角度は等しくなる性質があります。
直線が交わるときに、向かい合ってできる角を対頂角と呼ぶよ！
対頂角は必ず等しくなる性質があります。交わる直線の数が増えても、対頂角の角度は同じになる性質があるので、ぜひ覚えておきましょう。
それでは、対頂角の性質について確認しておこう！
「対頂角（たいちょうかく）の性質」について
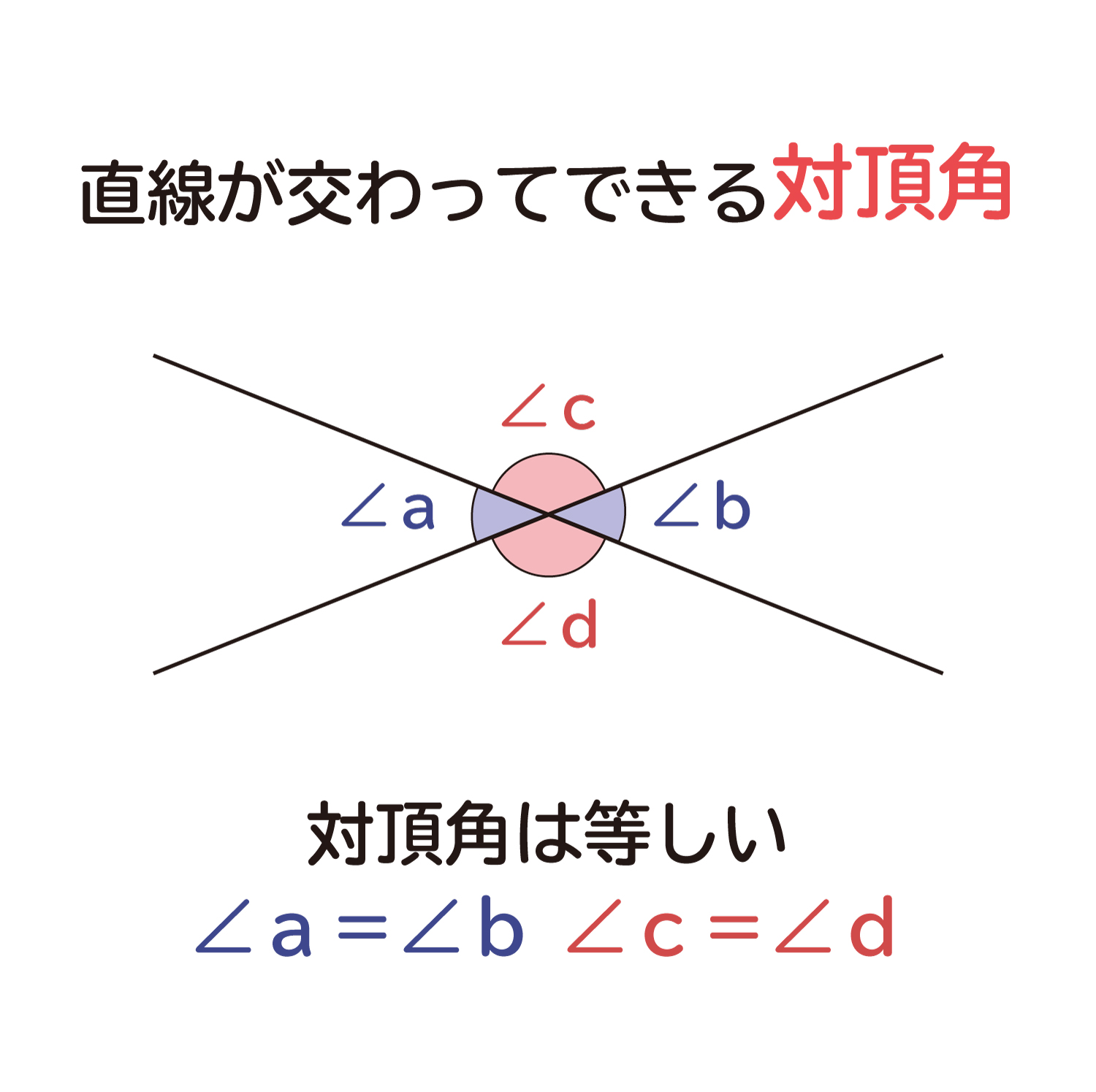
直前が交わるときに、向かい合ってできる角を対頂角と呼びます。下のような対頂角が出来ているとき、∠ａ＝∠ｂ、∠ｃ＝∠ｄとなります。
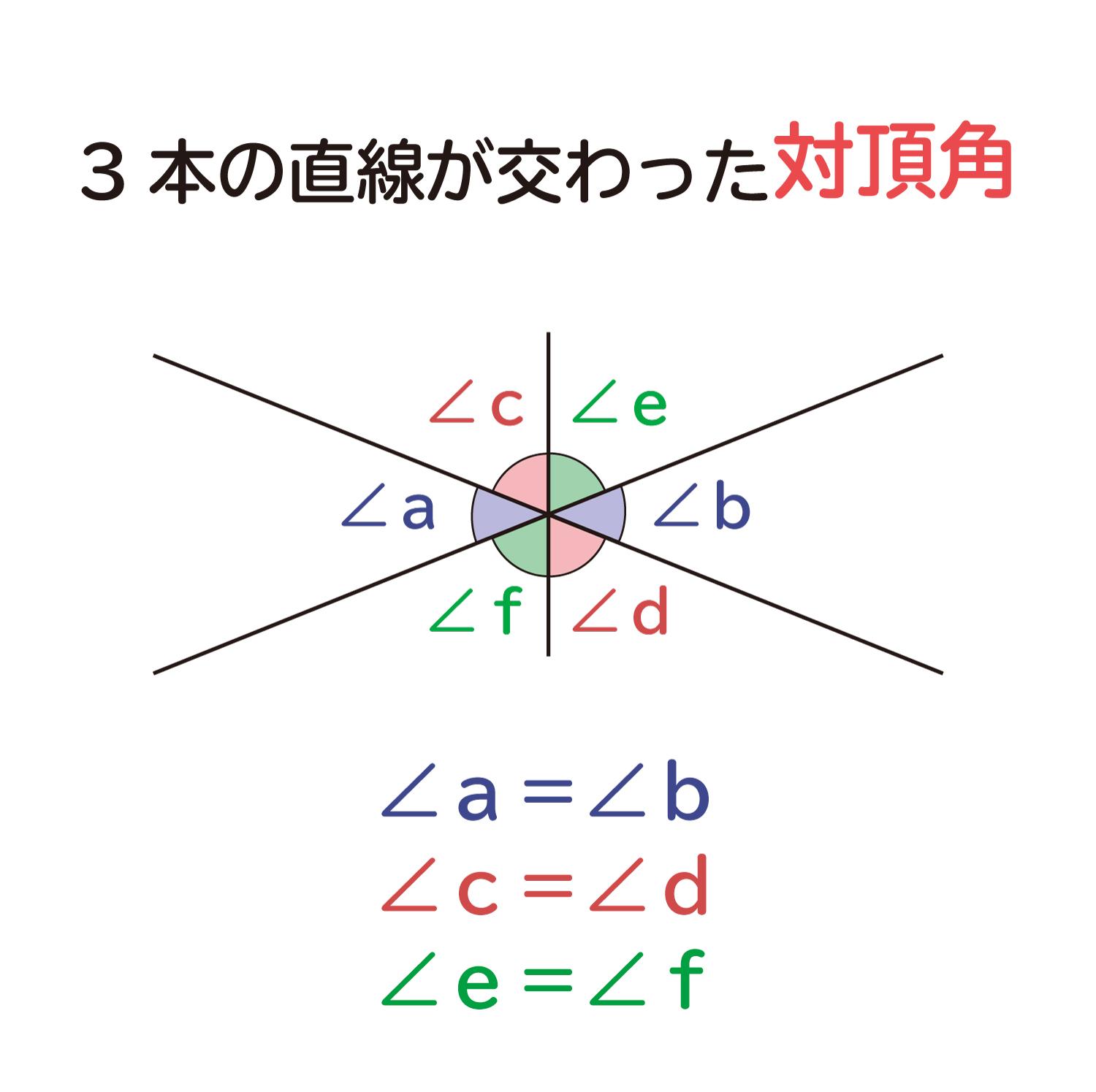
次に、交点で交わる直線が１本増えた時を考えてみます。下のように、３本の直線が１点で交わるときは、∠ａ＝∠ｂ、∠ｃ＝∠ｄ、∠ｅ＝∠ｆとなります。
交わる直線が３本に増えても、それぞれの角が対頂角の関係になっているね！
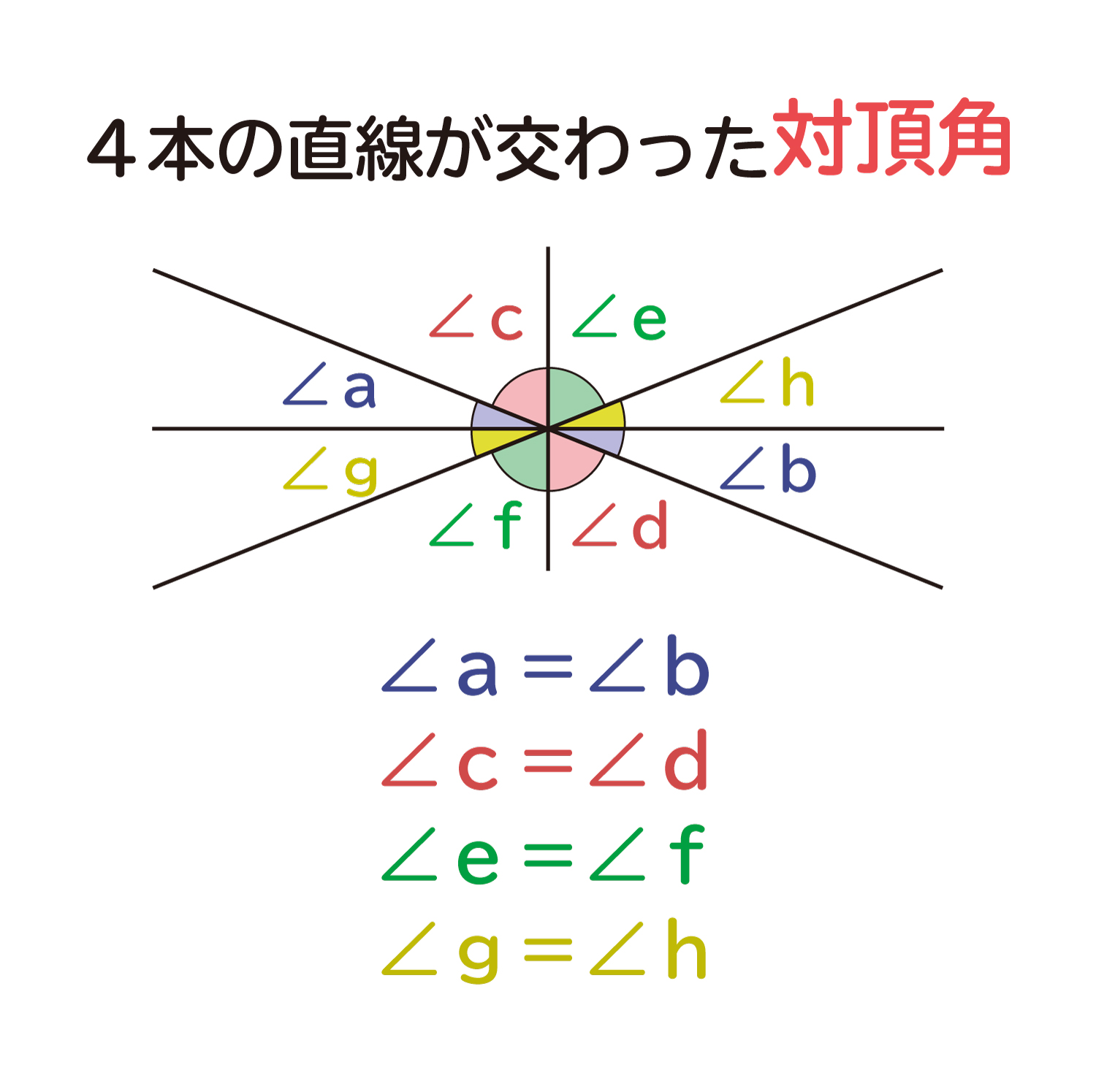
今度は、交わる直線が４本の時はどうでしょうか？下の図のように、４本の直線が１点で交わるとき、∠ａ＝∠ｂ、∠ｃ＝∠ｄ、∠ｅ＝∠ｆ、∠ｇ＝∠ｈとなります。
交わる直線が４本でも、それぞれに対頂角が出来るね！
このように、同じ点で交わる直線の数が増えても、それぞれ角度が等しい対頂角ができます。中学校の数学では図形問題で対頂角を使う問題が出てくるので、ぜひ覚えておいてくださいね。
まとめ
・直線が交わるときに、向かい合ってできる角を「対頂角」と呼びます。
・交わる直線の数が増えても、できる対頂角の角度は等しくなります。
直線が交わったときにできる対頂角の性質は、ぜひ覚えておいてね！
その他の中学生で習う公式は、こちらのリンクにまとめてあるので、気になるところはぜひ読んでみて下さいね。