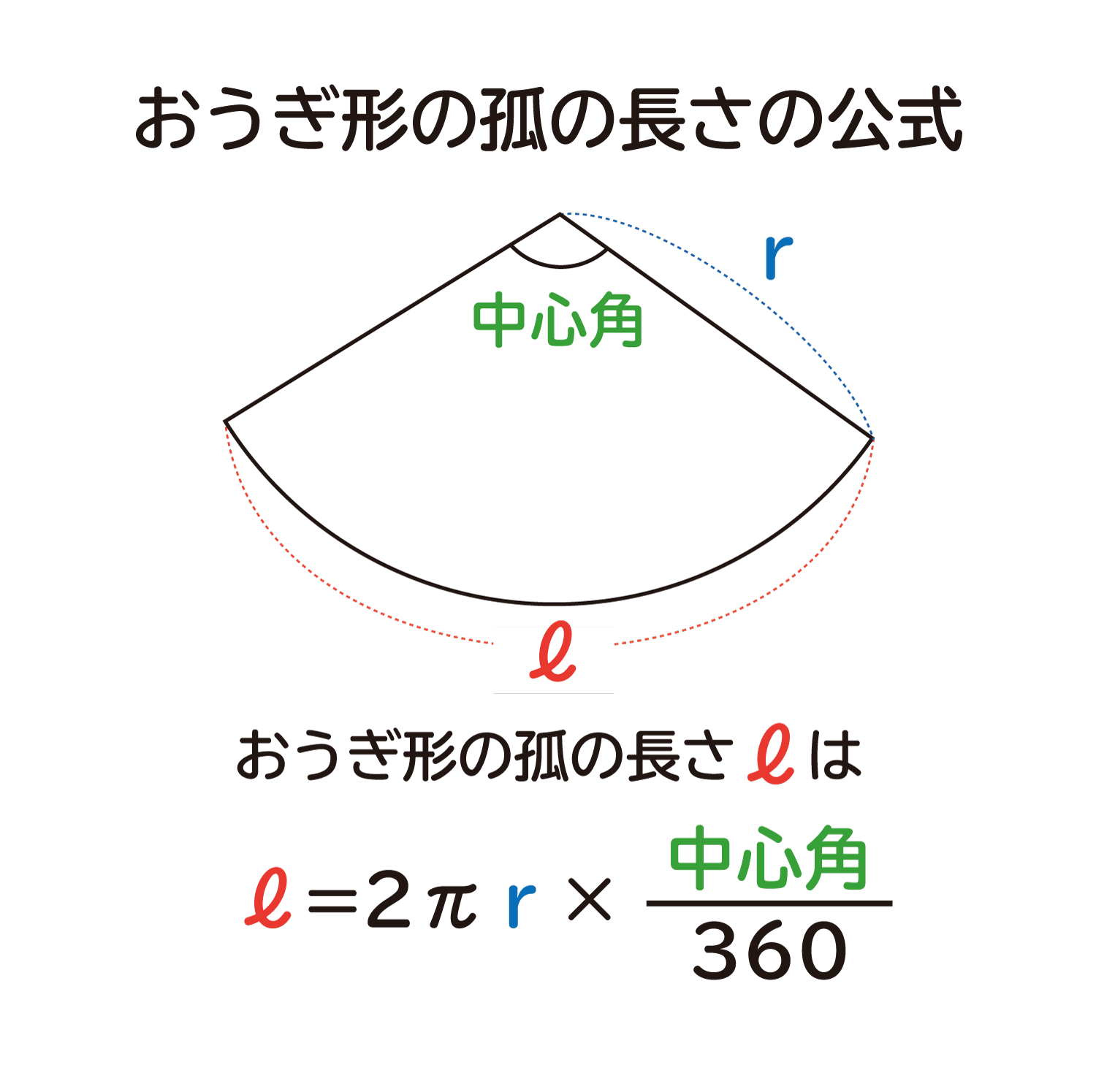
ここではなぜ、おうぎ形の孤の長さは「２πｒ×中心角／３６０」で求めることができるのか？を考えていきたいと思います。
この公式のポイント
・おうぎ形の孤の長さは「２πｒ×中心角／３６０」で求めることができます。
・おうぎ形の半径をｒ、中心角をａとしたとき、孤の長さＬは下の公式で書くことができます。
$$\Large{l}=2πr×\frac{a}{360}$$
中学生では、おうぎ形の孤の長さを求めるときに、この公式を使って解く問題が出てきます。おうぎ形の孤の長さを求める式は、なぜ上のような計算になっているのか忘れてしまったときに、ぜひ参考にしてみて下さい。
「おうぎ形の孤の長さは、２πｒ×中心角／３６０」になる説明
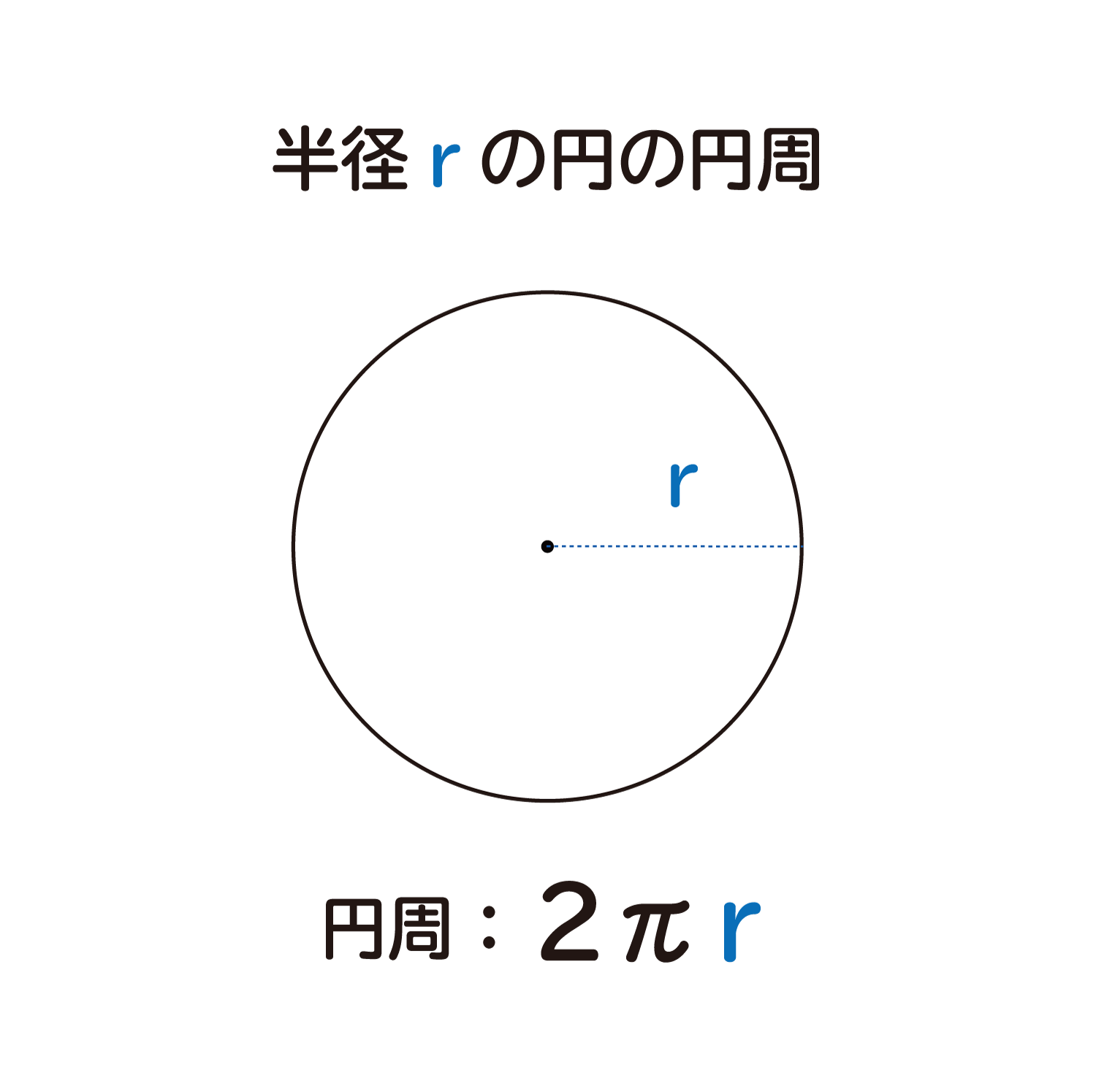
はじめに、半径ｒの円の「円周」の式を確認します。
円の円周の式
$$\Large{2}{π}{r}$$
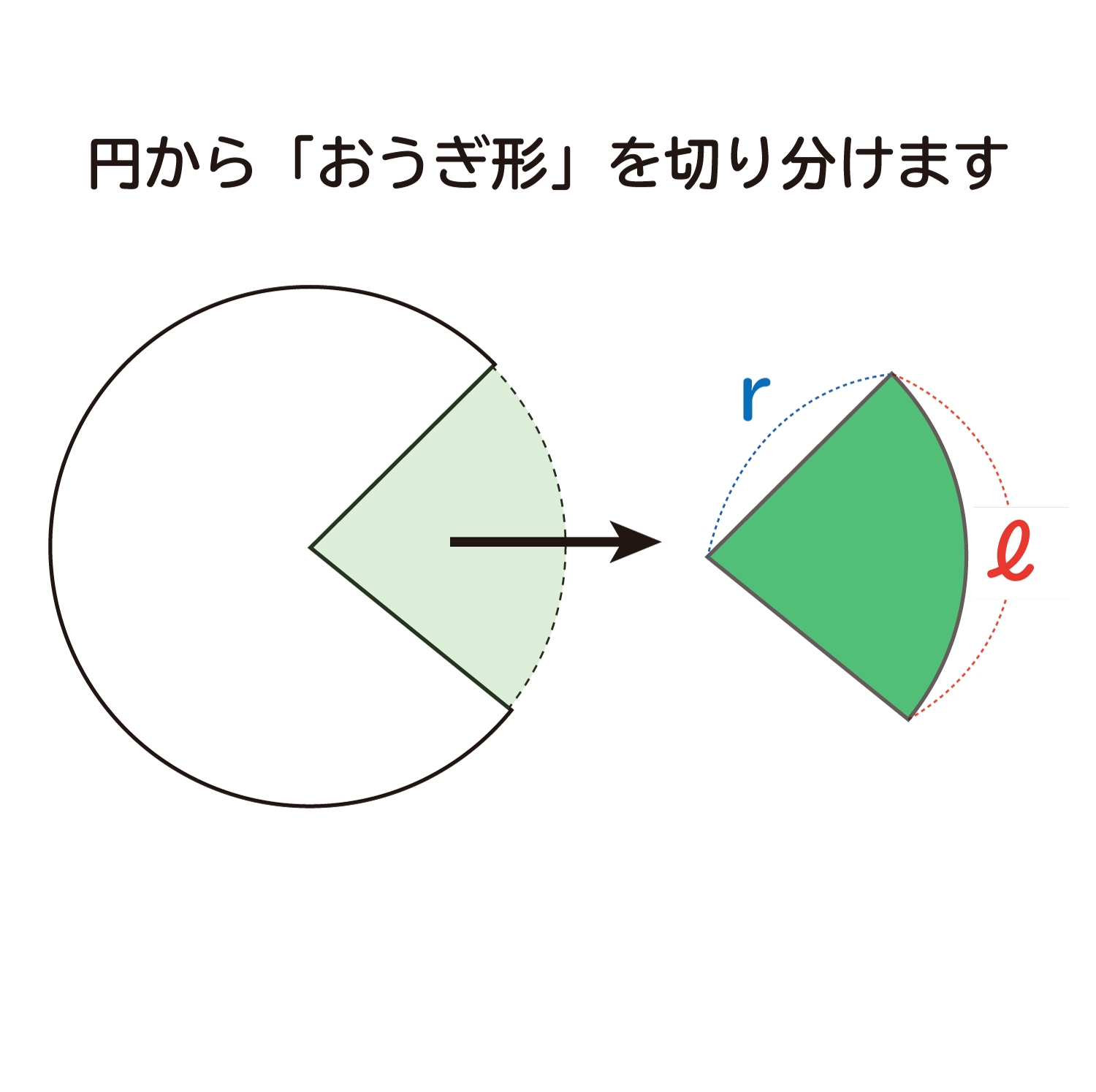
次に下の図のように、この円を一部を切っておうぎ形を作ったとき、おうぎ形の孤の長さは、この円の全体の円周の割合になっているでしょうか？
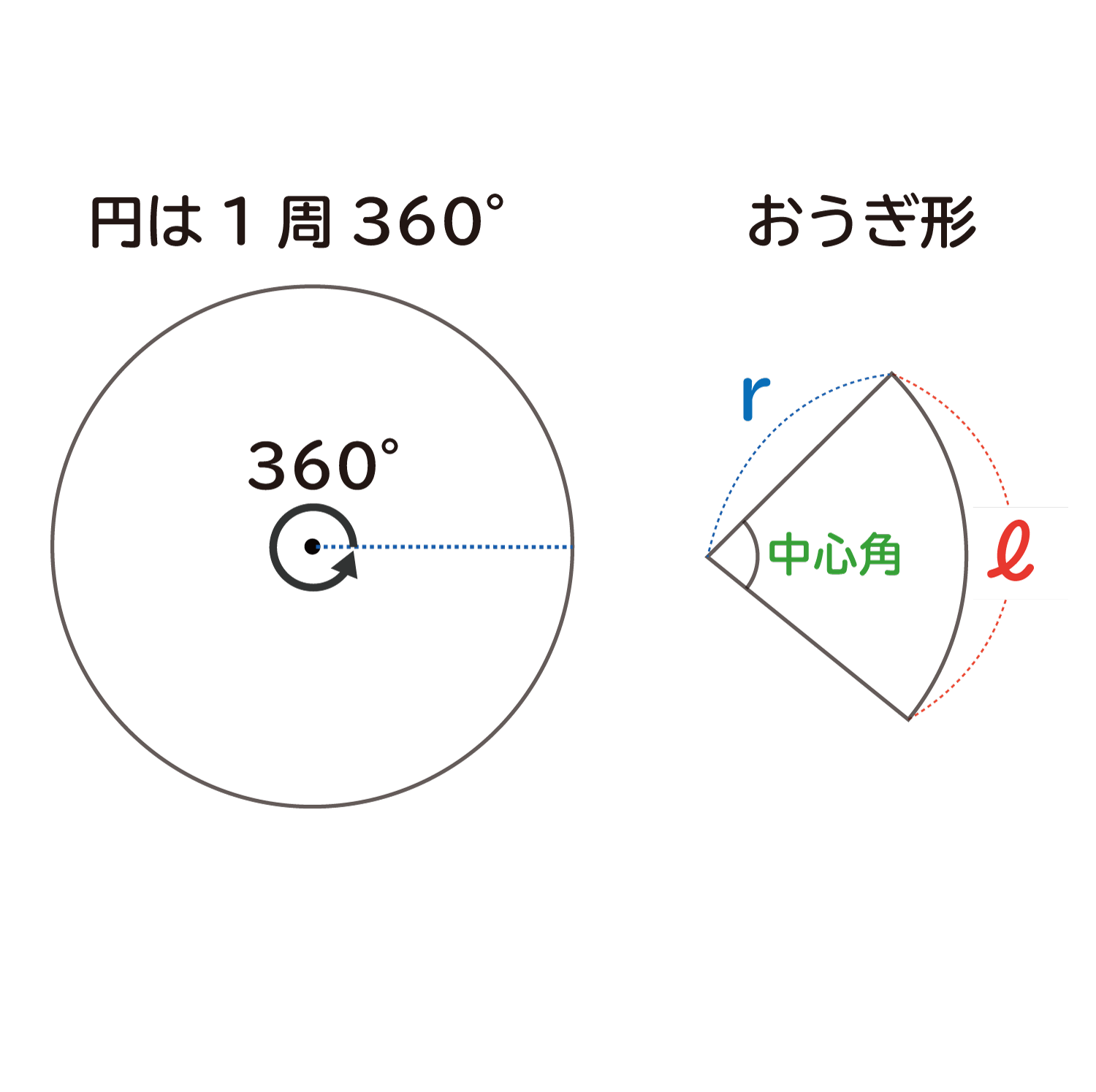
ここで、おうぎ形が元の円の何割か？を出すために、中心角ａの大きさを使います。円の１周３６０度に対する、おうぎ形の中心角の大きさ割合は、おうぎ形の中心角の大きさをａとすると、円の３６０で割って下の式で求めることができます。
$$\Large\frac{a}{360}$$
円に対するおうぎ形の割合が上の式になるので、これに円の円周に掛けると、おうぎ形の孤の長さを求めることができます。
$$\Large{2πr}×\frac{a}{360}$$
まとめ
・おうぎ形の孤の長さを求めるには、おうぎ形がその元の円の何割にあたるかを考えます。
・上の割合を出すためには、おうぎ形の中心角の大きさを、円の1周の角度３６０°で割れば割合を出すことができます。
・円の円周に、おうぎ形の中心角の割合を掛けると、おうぎ形の孤の長さを求めることができます。
その他の中学生で習う公式は、こちらのリンクにまとめてあるので、気になるところはぜひ読んでみて下さいね。