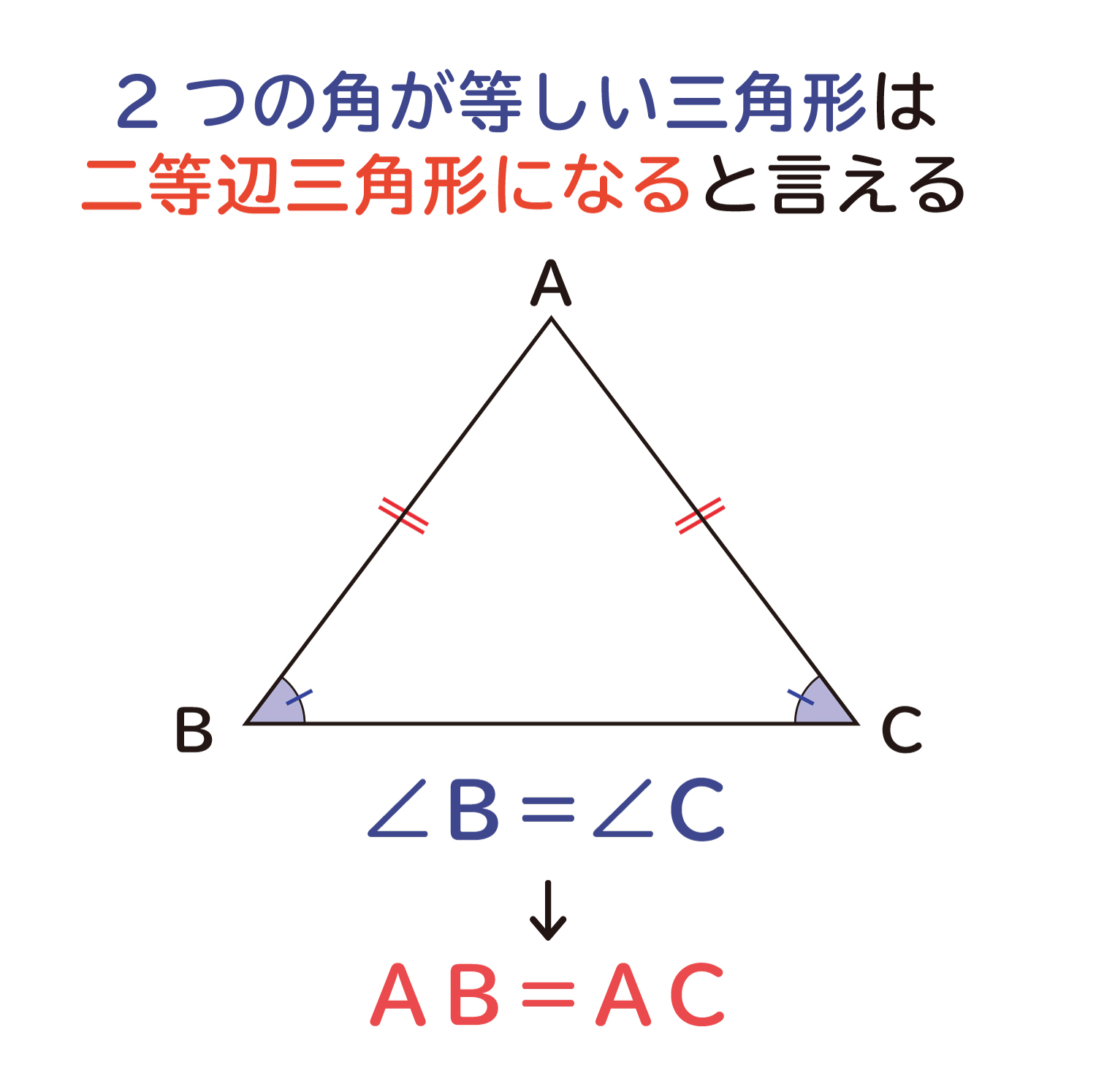
 二等辺三角形は、「2つの辺の長さが等しい三角形」と定義されています。そして、二等辺三角形は2つの辺が等しいことで、2つの角も等しくなる性質を持っています。
二等辺三角形は、「2つの辺の長さが等しい三角形」と定義されています。そして、二等辺三角形は2つの辺が等しいことで、2つの角も等しくなる性質を持っています。
ここでは、逆に2つの角が等しい三角形があるとき、その三角形は二等辺三角形(2つの辺の長さが等しい三角形)になるか?を確認していきたいと思います。
この公式のポイント
・二等辺三角形は「2つの辺が等しい三角形」と定義されます。
・二等辺三角形は「2つの角が等しくなる」という性質があります。
・今回は2つの角が等しい三角形は、二等辺三角形(2つの辺が等しい三角形)になることを確認します。

二等辺三角形は2つの辺の長さが等しいことで、いくつかの性質が出てきます。二等辺三角形の性質については、下のリンクにまとめているので、参考にしてみて下さいね。
参考:二等辺三角形の性質「2つの角は等しくなる」ことについて
-
-
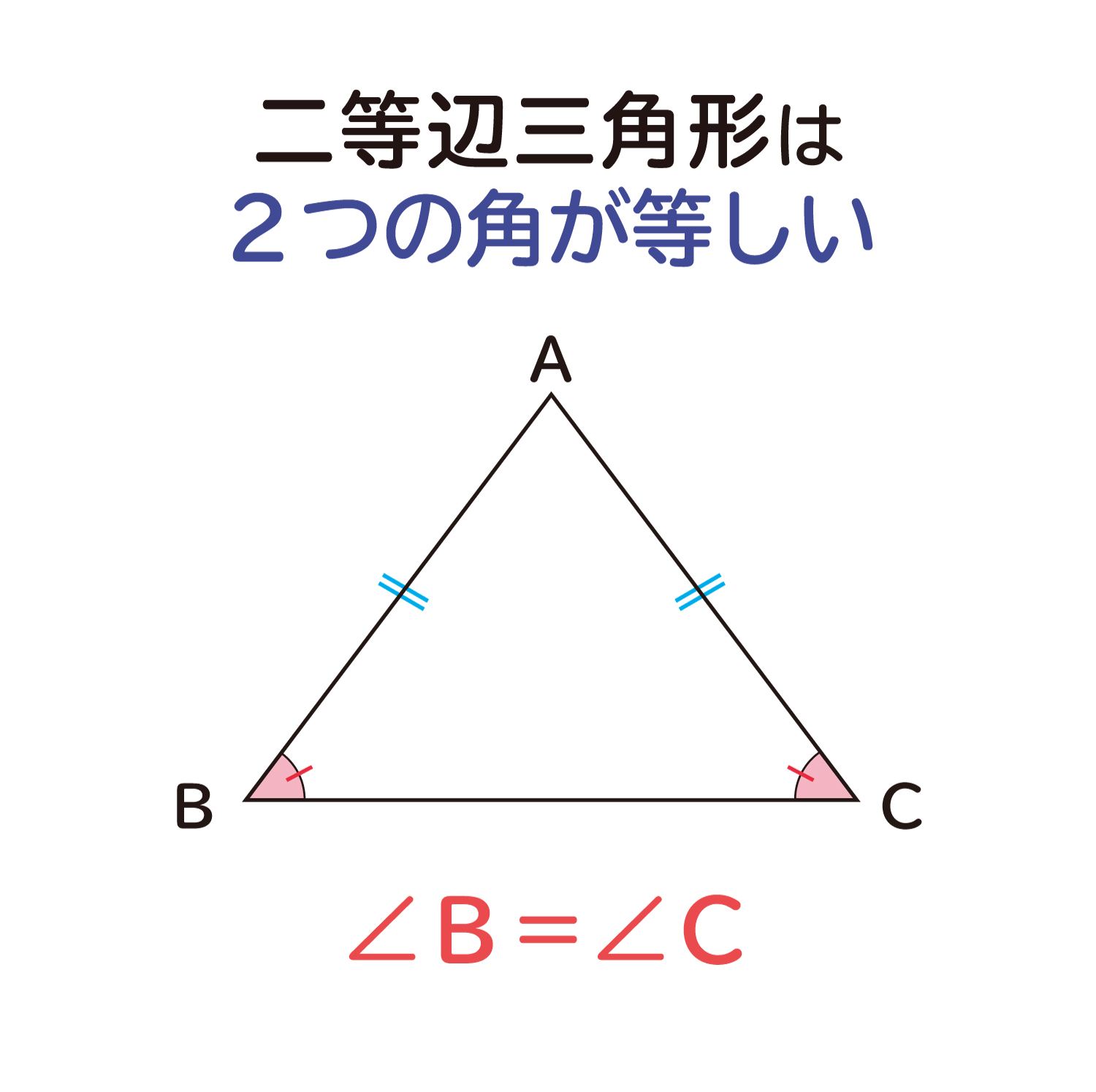
”二等辺三角形の2つの角は等しくなる”ことの説明
二等辺三角形は、「2つの辺の長さが等しい三角形」と定義されます。 二等辺三角形は2つの辺の長さが等しいことでさまざまな性質が現れてきます。そ ...
続きを見る
参考:二等辺三角形の性質「頂角の二等分線は、底辺を垂直に二等分する」ことについて
-
-
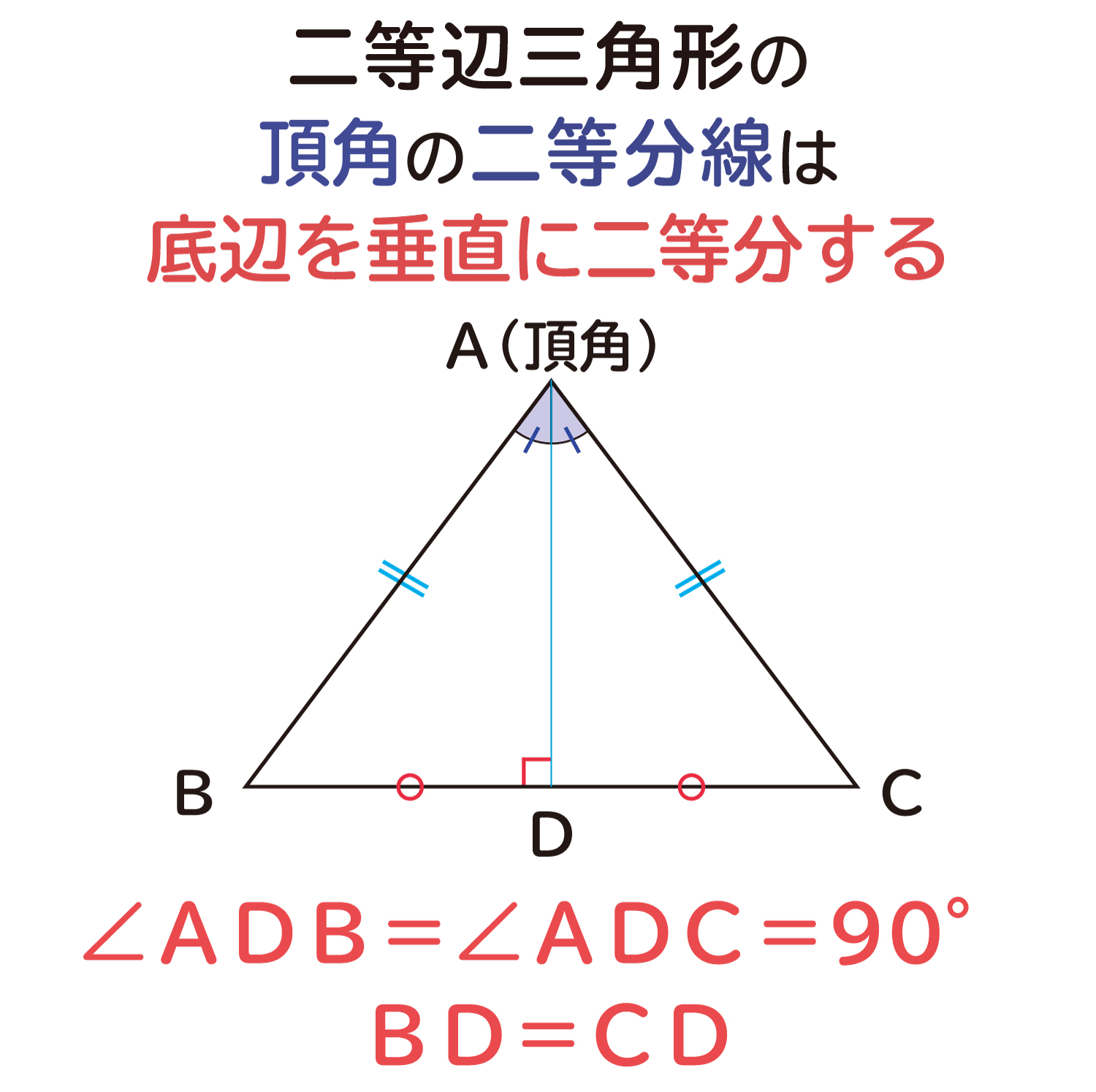
”二等辺三角形の頂角の二等分線は、底辺を垂直に二等分する”ことの説明
二等辺三角形は、「2つの辺の長さが等しい三角形」と定義されます。 二等辺三角形は2つの辺の長さが等しいことでさまざまな性質が現れてきます。そ ...
続きを見る

「2つの角が等しい三角形は、二等辺三角形になる」ことの説明
下の図のように、∠B=∠Cという2つの角が等しい三角形を考えます。ここで、∠Aの二等分線(Aの角度を2つに等しく分ける直線です)を引き、この直線と辺BCの交点を点Dとします。
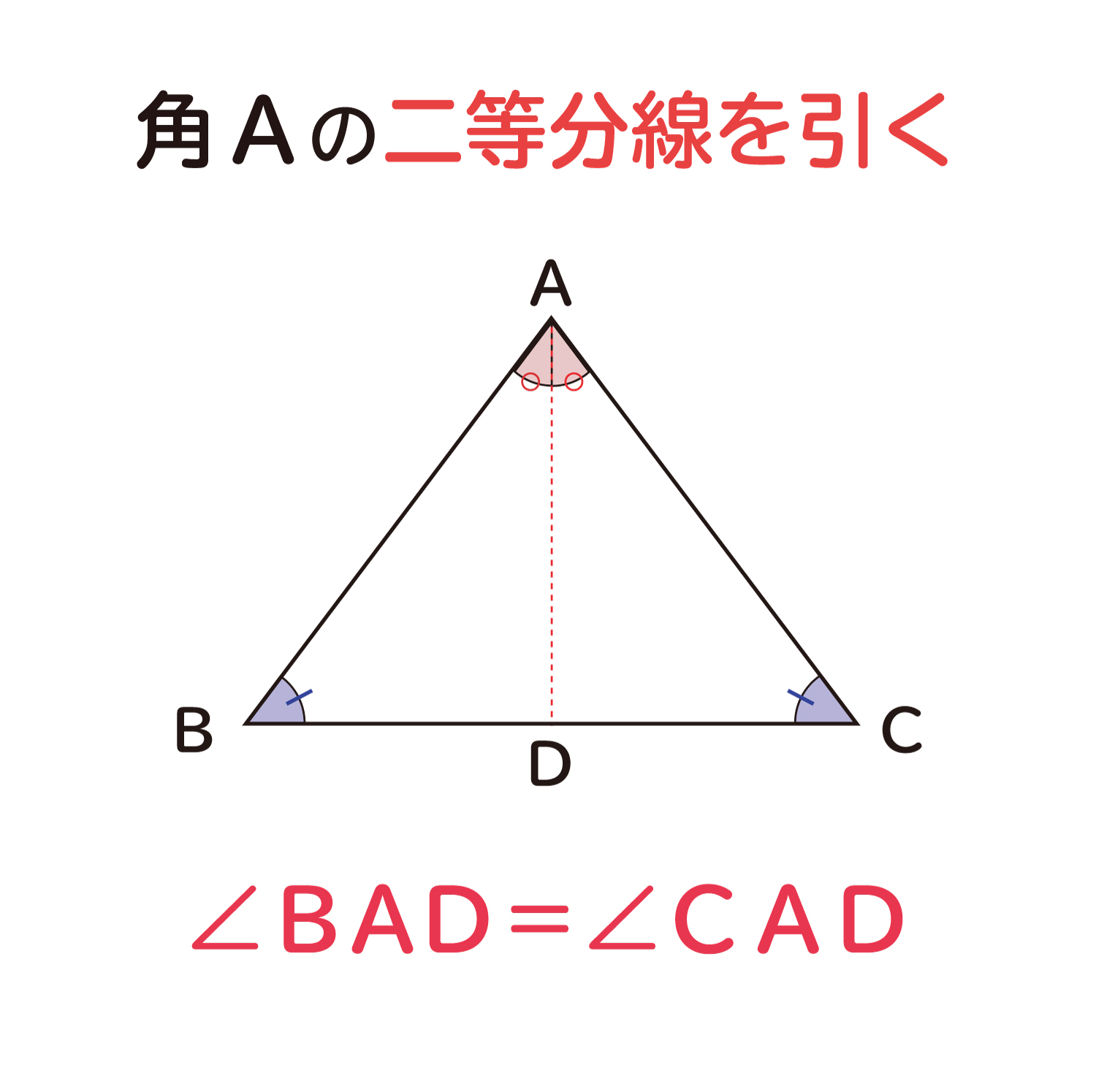
ここで、三角形の内角の和は180°となるので、
△ABDにおいて、∠ADB=180°ー∠B-∠BAD
△ACDにおいて、∠ADC=180°-∠C-∠CAD
このとき、∠B=∠C、∠BAD=∠CADとなっているので、∠ADB=∠ADCになると言うことが出来ます。
以上のことから、△ABDと△ACDは、1辺(AD)が共通でその両端の角が等しいことから合同な三角形と言えます。△ABD≡△ACD
そして、合同な三角形は、対応する辺は等しくなるので、AB=ACとなります。

まとめ
・2つの角が等しい三角形は、二等辺三角形になることが言えます。
・1つの角を二等分する直線を引くと、2つの合同な三角形を作ることができます。
・合同な三角形の対応する辺は等しいので、2つの辺が等しい二等辺三角形であることが言えます。

「中学2年生の公式の解説」一覧
- 連立方程式の解き方の説明ー代入法を使った解き方ー
- 連立方程式の解き方の説明ー加減法を使った解き方ー
- 直線が交わるときにできる対頂角の性質
- 平行線の同位角と錯角の性質
- 「三角形の1つの外角は、それと隣り合わない2つの内角の和に等しい」ことの説明
- 「n角形の内角の和は、" 180°×(n-2)”」になる説明
- 「n角形の外角の和は 360° 」になる説明
- 三角形の合同条件の説明
- ”二等辺三角形の2つの角は等しくなる”ことの説明
- ”二等辺三角形の頂角の二等分線は、底辺を垂直に二等分する”ことの説明
- ”2つの角が等しい三角形は、二等辺三角形になる”ことの説明
- 直角三角形の合同条件の説明
- ”平行四辺形の対辺の長さは等しくなる”ことの説明
- ”平行四辺形の対角の角度は等しくなる”ことの説明
- ”平行四辺形の対角線は中点で交わる”ことの説明
