ここではなぜ、おうぎ形の面積は「１／２×弧の長さ×半径」で求めることができるのか？を考えていきたいと思います。
この公式のポイント
・おうぎ形の面積は「１／２×弧の長さ×半径」で求めることができます。
・おうぎ形の半径をｒ、弧の長さをＬとしたとき、面積Ｓは下の公式で書くことができます。
$$\Large{S}=\frac{1}{2}{l}{r}$$
中学生では、円すいの表面積を求めるときに、この公式を使って解く問題が出てきます。円すいの側面は、広げるとおうぎ形の形をしています。
おうぎ形の面積を求める公式を忘れてしまったときに、ぜひ参考にしてみて下さい。
メモ
おうぎ形の面積は、半径と中心角の大きさを使っても求めることが出来ます。※孤の長さを使わないで面積を求める公式です。もう一つの公式については、こちらの記事に解説を書いているので、参考にしてみて下さい。
-
-
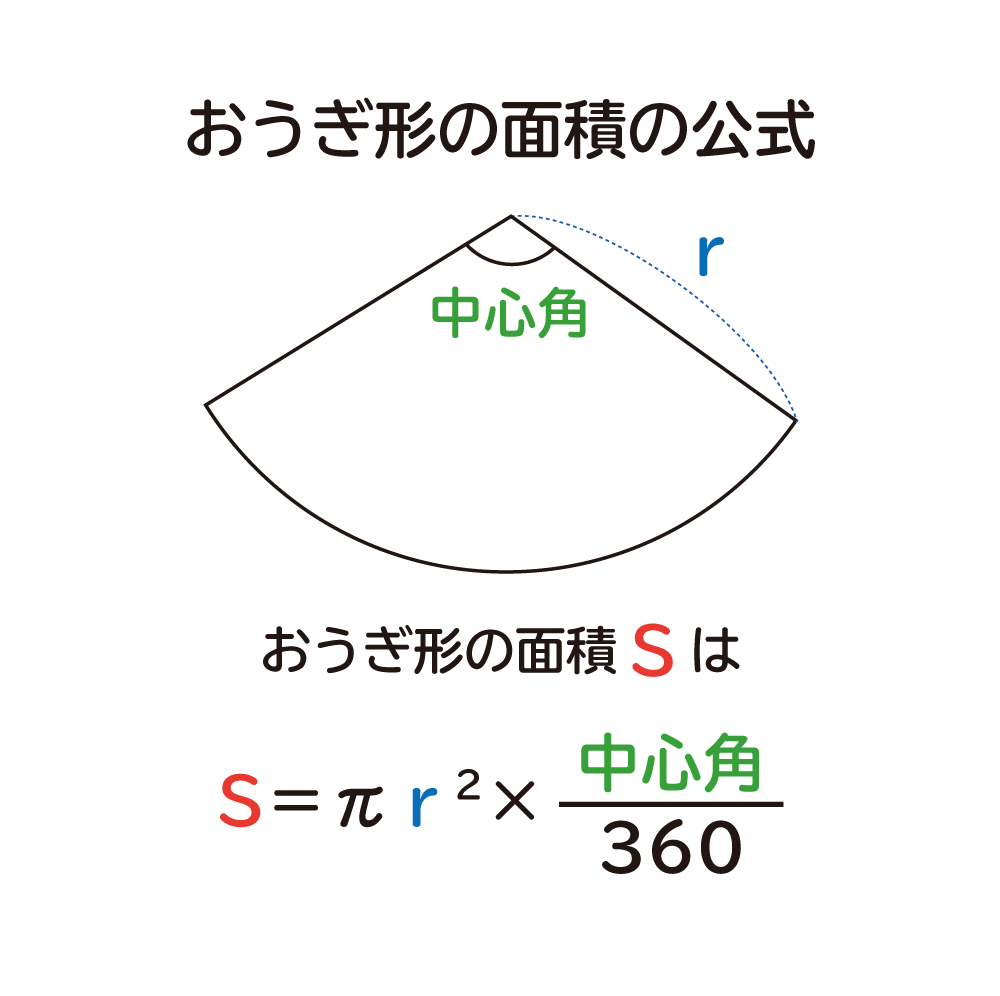
「おうぎ形の面積は " π×半径×半径×中心角／３６０ ”」になる説明
ここではなぜ、おうぎ形の面積は「π×半径×半径×中心角／３６０」で求めることができるのか？を考えていきたいと思います。 この公式のポイント ...
続きを見る
「おうぎ形の面積は、１／２×弧の長さ×半径」になる説明
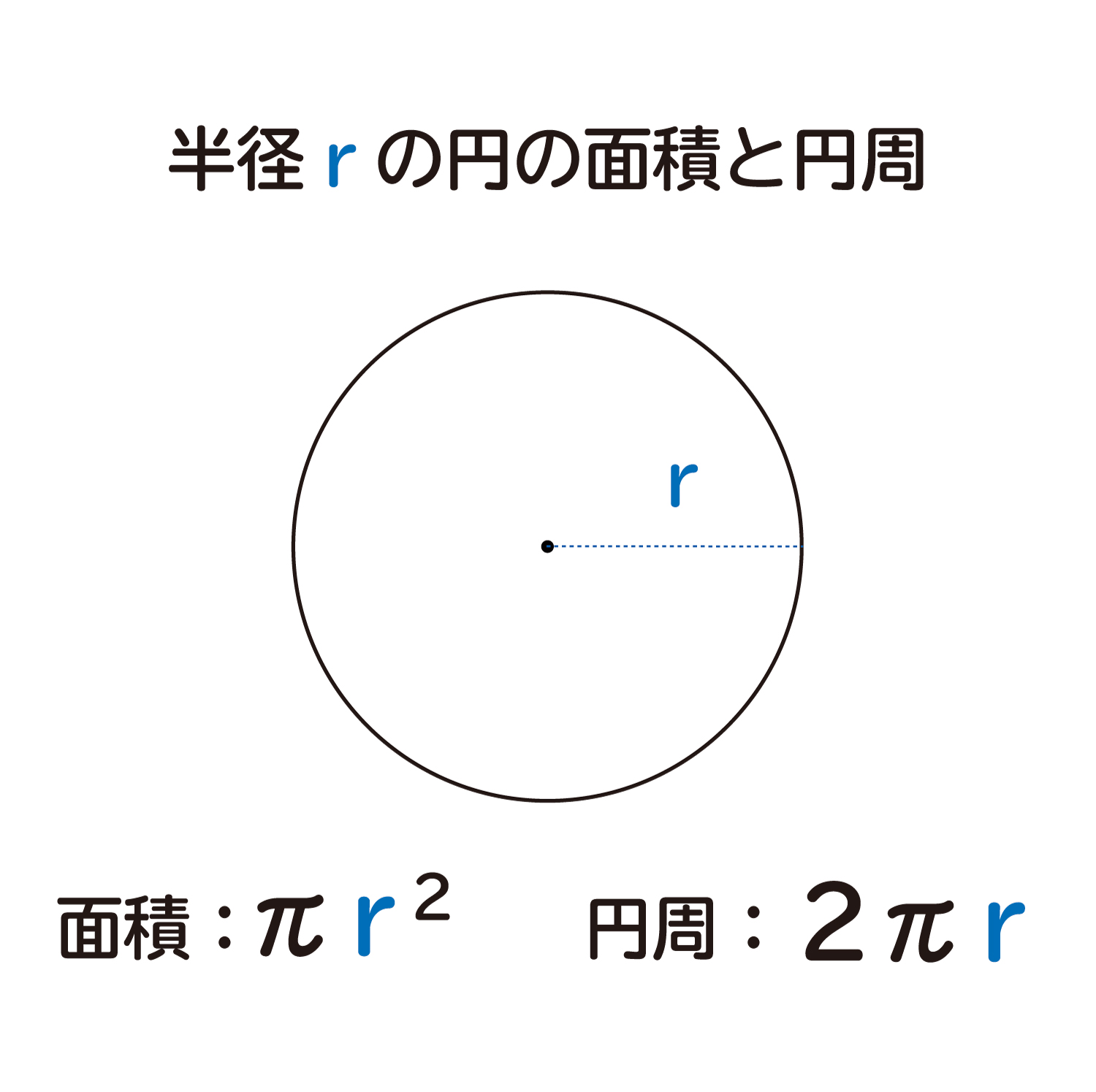
まずはじめに、半径ｒの円の「面積」と「円周」の式を確認しておきます。
円の面積の式
$$\Large{π}r^2$$
円の円周の式
$$\Large{2}{π}{r}$$
次に下の図のように、この円を一部を切っておうぎ形を作ったとき、おうぎ形の面積は、円の全体の面積の割合になっているでしょうか？
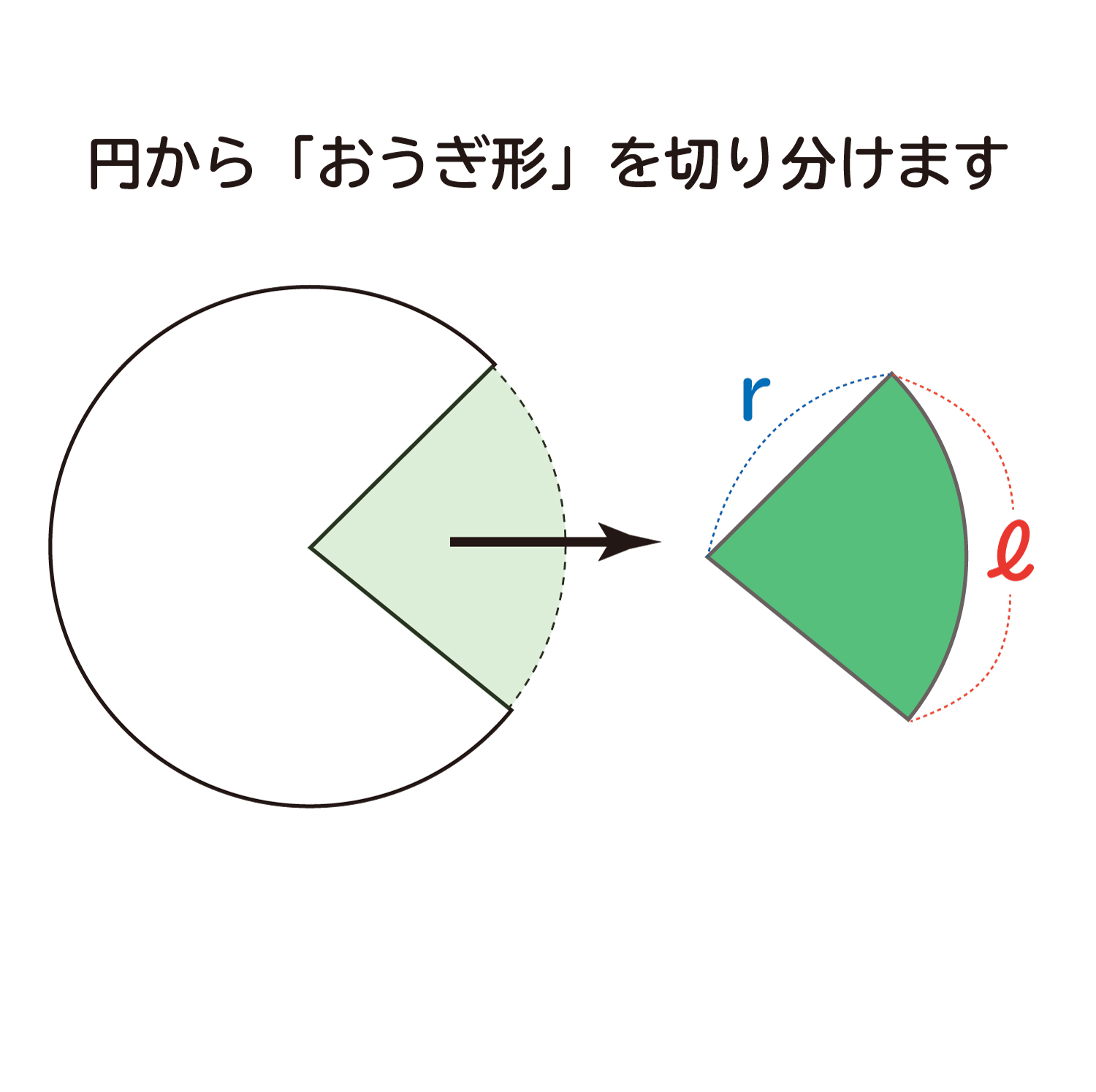
ここで、おうぎ形が元の円の何割か？を出すために、弧の長さを使います。円全体の円周に対する、おうぎ形の弧の長さの割合は、おうぎ形の弧の長さを、円周で割って下の式になります。
$$\Large\frac{l}{2πr}$$
円に対するおうぎ形の割合が上の式になるので、これに円の面積に掛けると、おうぎ形の面積を求めることができます。
$$\Large{π}r^2×\frac{l}{2πr}$$
$$\Large＝\frac{1}{2}{l}{r}$$
まとめ
・おうぎ形の面積は、おうぎ形をつくる元の円の面積の何割になるかを考えます。
・上の割合を出すためには、おうぎ形の弧の長さを、円の円周で割れば割合を出すことができます。
・円の面積に、おうぎ形の面積の割合を掛けると、おうぎ形の面積を求めることができます。