《 中学生 数学 》公式の解説

「ｎ角形の内角の和は、" １８０°×（ｎ－２）”」になる説明

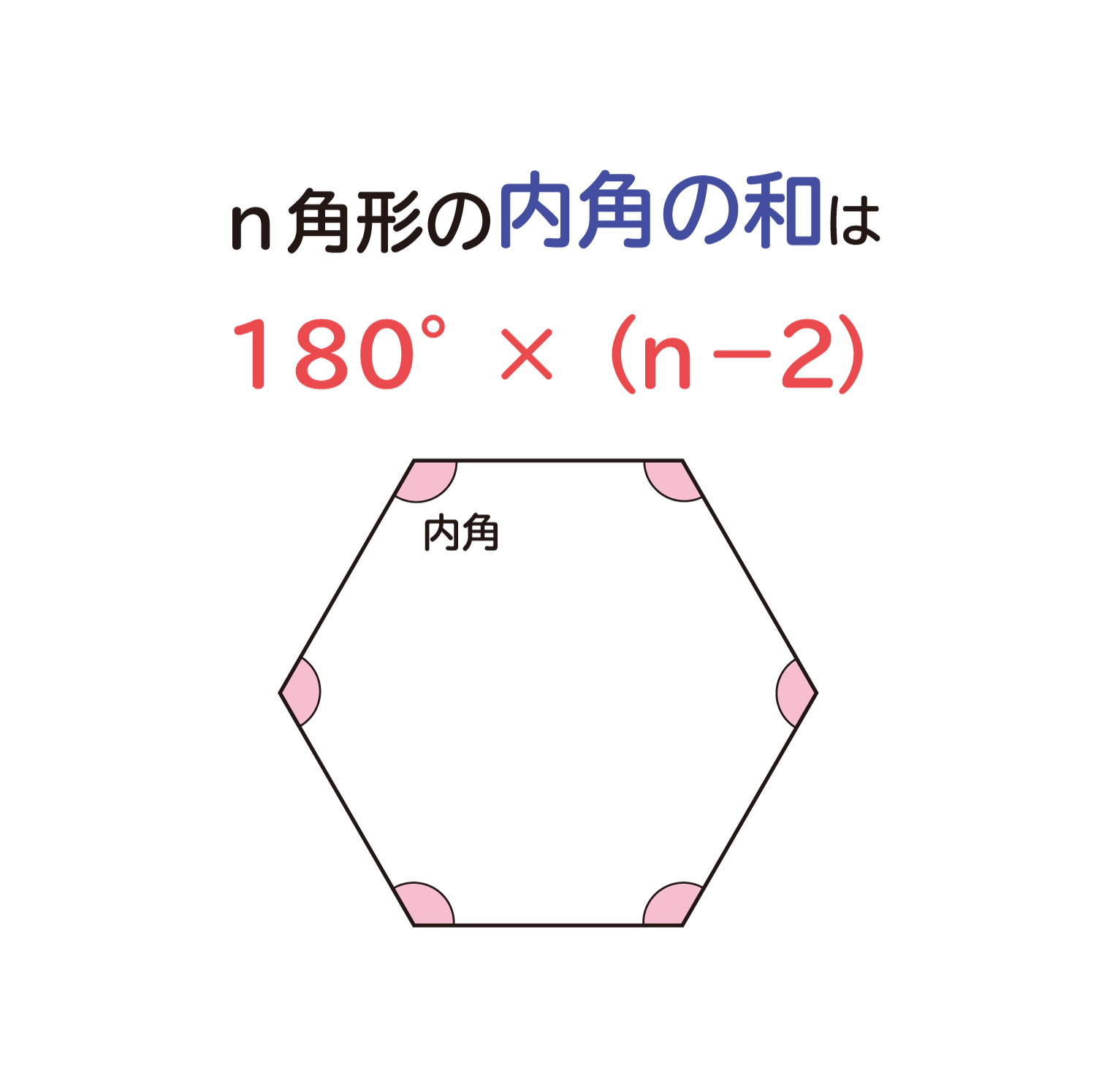
なぜ、”ｎ角形の内角の和は、180°×（ｎ－１）”なのか？の説明図１ここではなぜ、ｎ角形の内角の和は「１８０°×（ｎ－２）」で求めることができるのか？を確認していきたいと思います。

この公式のポイント

・ｎ角形の内角の和は、１８０°×（ｎ－２）で求めることが出来ます。

・この公式を理解するためには、三角形の内角の和は１８０°という公式を使います。

このｎ角形の内角の和の公式は、中学生で習う内容です。ただ、実は小学生でも多角形の内角の和について習っているので、その復習にもなっている公式です。

ぴよ校長
小学生で習った多角形の内角の和については、覚えているかな？

中学生では、多角形の角の数を「ｎ」として書き表すことが違いますが、その他の内容は小学生で習ったこととほとんど同じ内容です。小学生向けに多角形の内角の和について説明したページもあるので、ぜひ参考にしてみて下さいね。

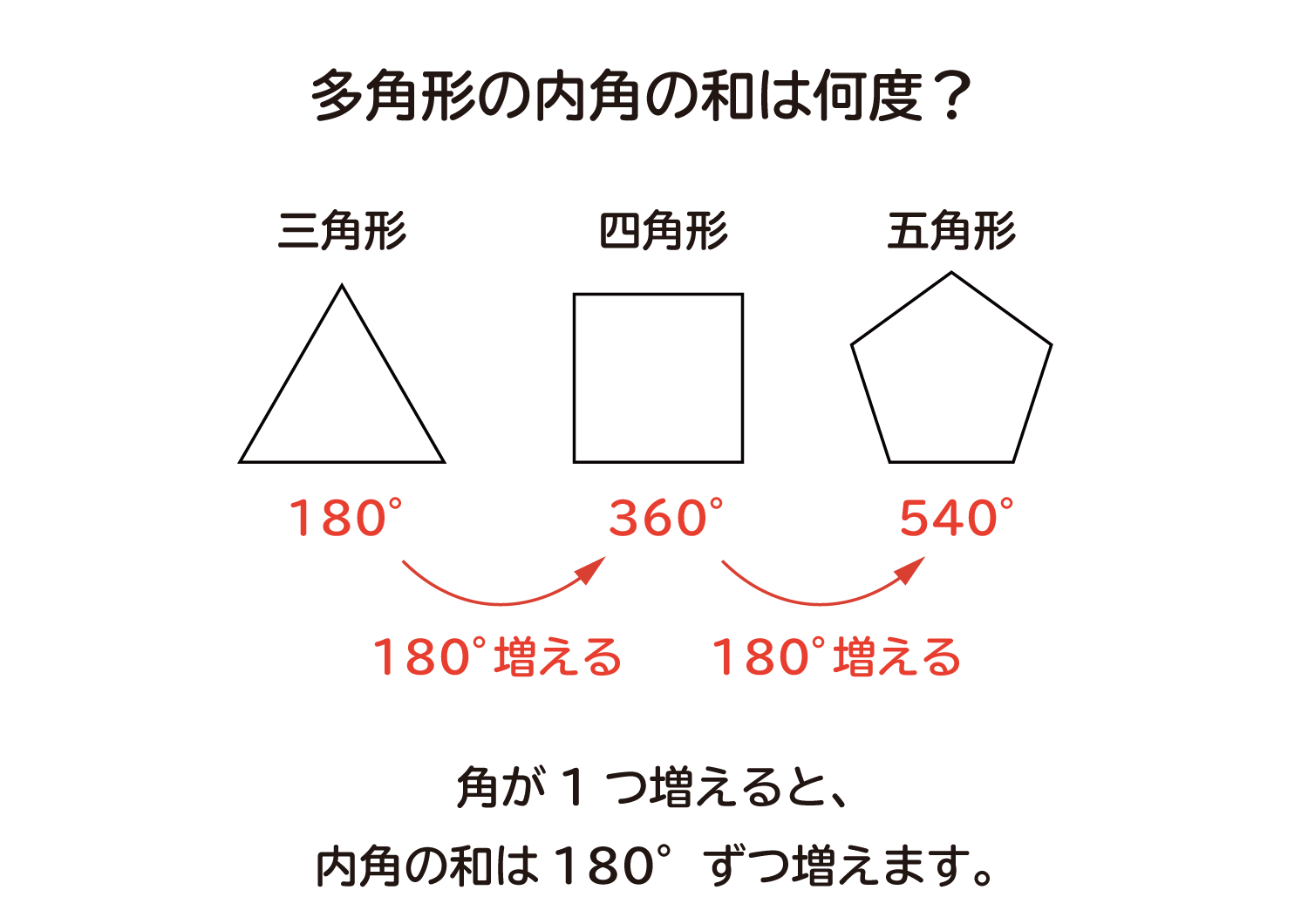
「多角形の内角の和は何度か？」の説明
「多角形の内角の和は何度か？」の説明

ここでは、多角形の内角の和は何度なのか？を、考えていきます。 上の図に少し説明を書いていますが、多角形は角が1つ増えるごとに、内角の和は18 ...

続きを見る
ぴよ校長
それではさっそく、ｎ角形の内角の和の公式を確認していこう！

「ｎ角形の内角の和は、１８０°×（ｎ－２）」となる説明

下の図のように三角形を１つ考えます。そしてこの三角形の外側に1つ点を加えて、この点から近い三角形の２つの頂点からこの点へ線を引くと、四角形ができることがわかります。そしてこの四角形の中には２つの三角形があります。

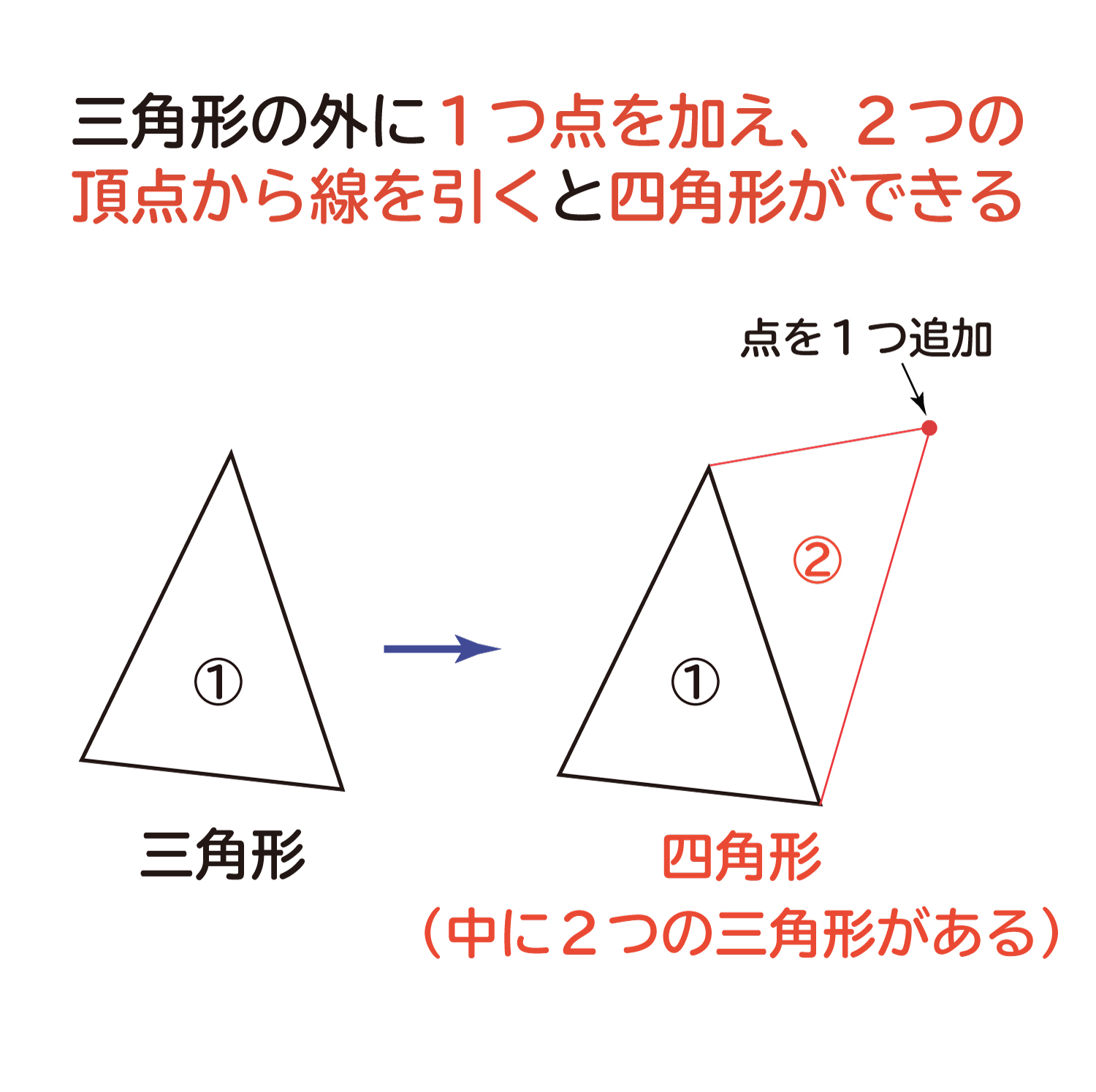
なぜ、”ｎ角形の内角の和は、180°×（ｎ－１）”なのか？の説明図２

更に外側に点を増やしながら、追加した点に線を引いていくと、できる多角形はどうなるでしょうか？下の図のように多角形の中にできる三角形の数も１つずつ増えていくことになります。

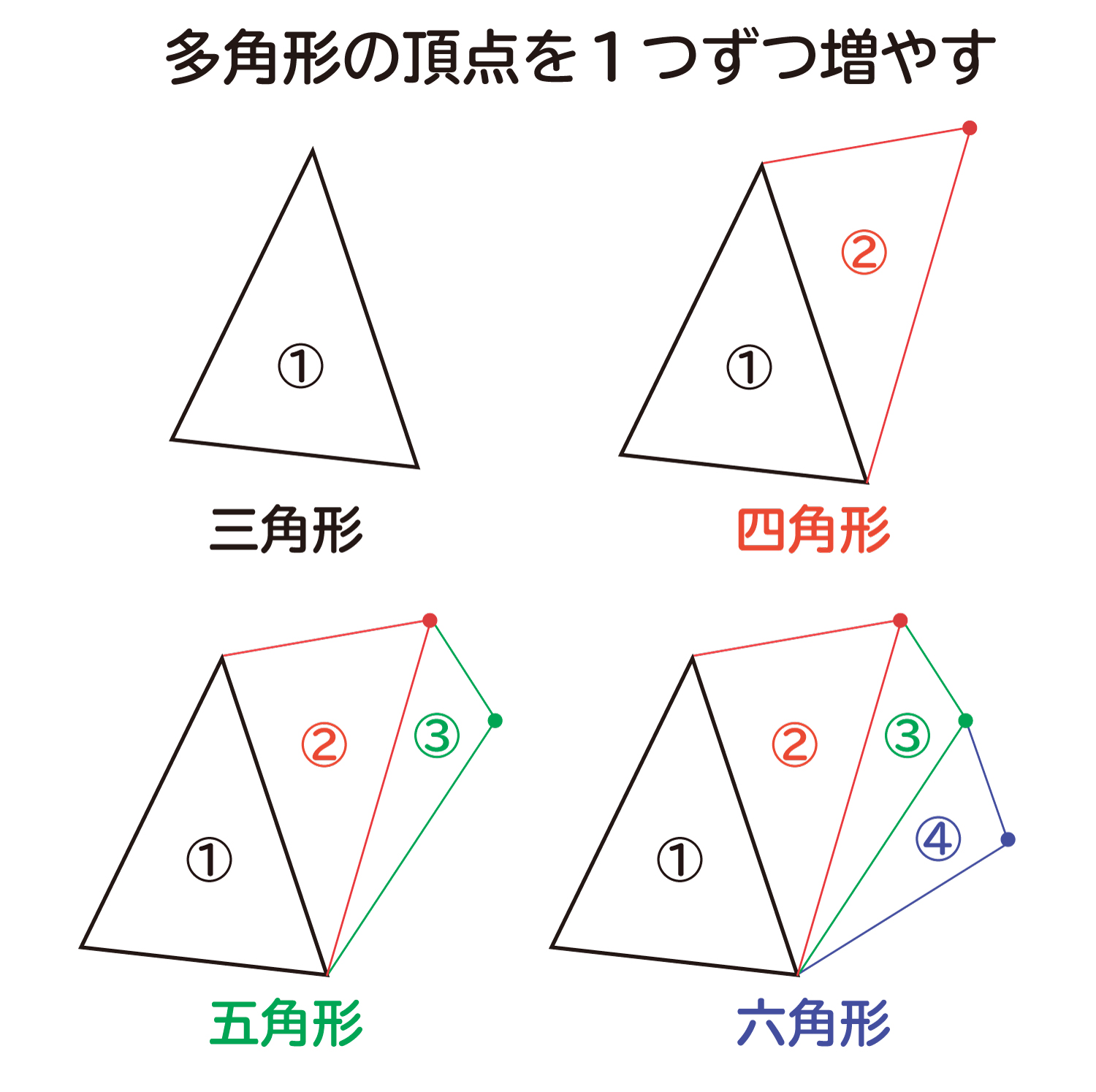
なぜ、”ｎ角形の内角の和は、180°×（ｎ－１）”なのか？の説明図３

この時、多角形の「頂点の数」とその中にできる「三角形の数」、「内角の和」は下の表のような関係になっています。

頂点の数 多角形の中にある三角形の数（頂点の数－２） 内角の和（１８０°×三角形の数）
三角形 ３つ １つ １８０°×１
四角形 ４つ ２つ １８０°×２
五角形 ５つ ３つ １８０°×３
・・・ ・・・ ・・・ ・・・
ｎ角形 ｎ （ｎ－２） １８０°×（ｎ－２）

多角形は頂点が１つ増えるごとに、中にできる三角形の数も１つずつ増えることが分かります。そして三角形の数は（頂点の数ー２）の数になっていることが分かります。

多角形の内角の和は「１８０°×三角形の数」で求めることが出来るので、ｎ角形の内角の和は１８０°×（ｎ－２）で求めることが出来ます。

ぴよ校長
ｎ角形の内角の和を出すことができたね！

まとめ

・ｎ角形は、その中に（ｎ－２）個の三角形があります。

・三角形の内角の和は１８０°なので、ｎ角形の内角の和は、１８０°×（ｎ－２）で求めることが出来ます。

ぴよ校長
ｎ角形の内角の和の公式を覚えることが出来たかな！

「中学2年生の公式の解説」一覧

-《 中学生 数学 》公式の解説