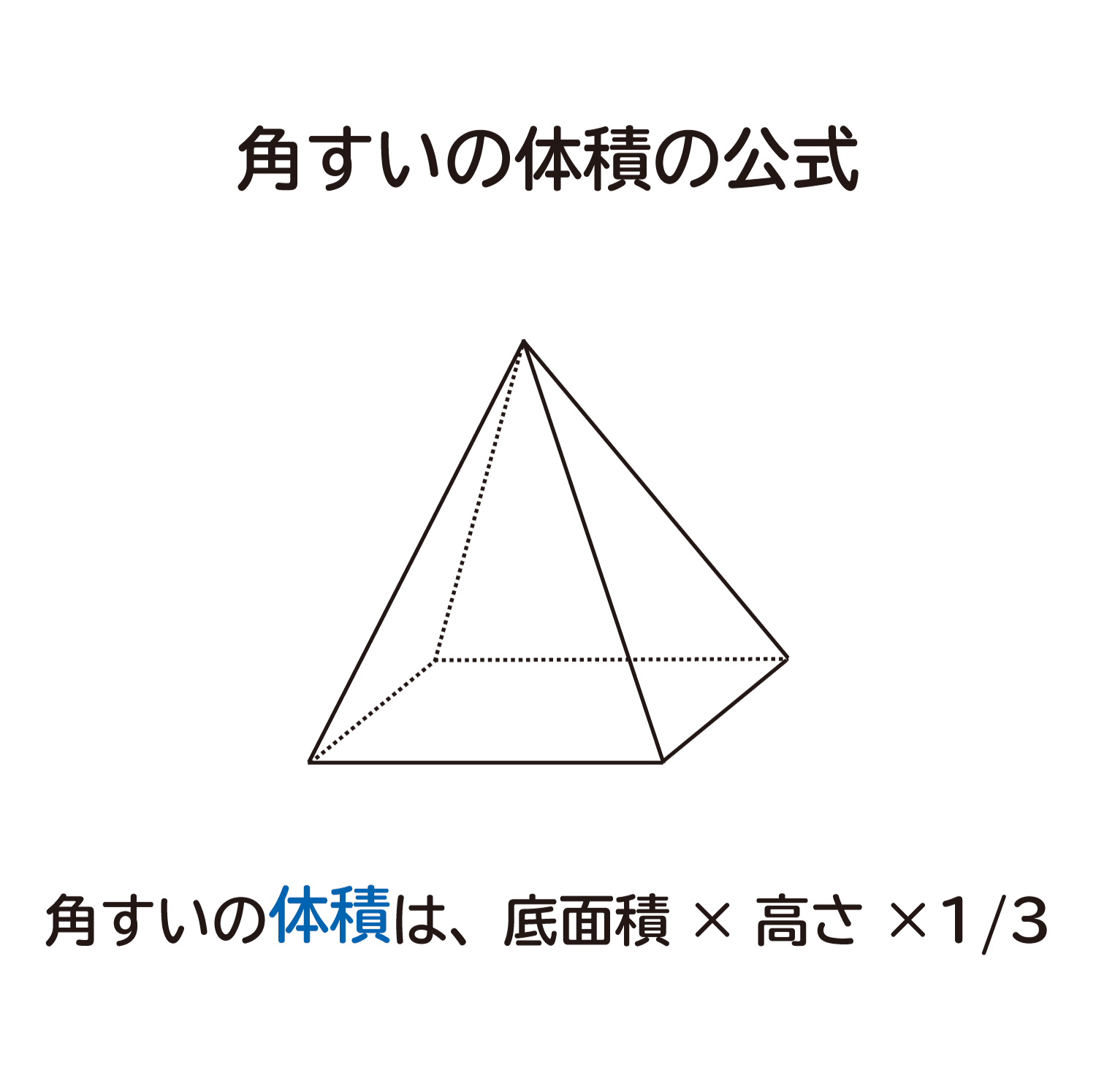
ここでは、なぜ角すいの体積は「底面積×高さ×１／３」なのか？を考えていきます。
この公式のポイント
・角柱の体積は「底面積×高さ」で求めることができます。
・角すいの体積は「底面積×高さ×１／３」で求めることができます。
・つまり、角すいの体積は、角柱の１／３になっています。
中学生では、角すいの体積の公式は「底面積×高さ×１／３」として習いますが、なぜ1/3なのか？については詳しい説明はありません。実際にこの公式をちゃんと説明するためには、高校で習う微分・積分を使う必要があるため、中学生ではそれを説明するのが難しい部分があります。
ここでは、厳密な証明ではありませんが、中学生が見て感覚的に理解しやすいように、図を使って説明してみたいと思います。
角すいの公式に１／３が出てくることに、少し疑問を持ったときに、ぜひ参考にしてみて下さいね。
「角すいの体積は、角柱の１／３」になる説明
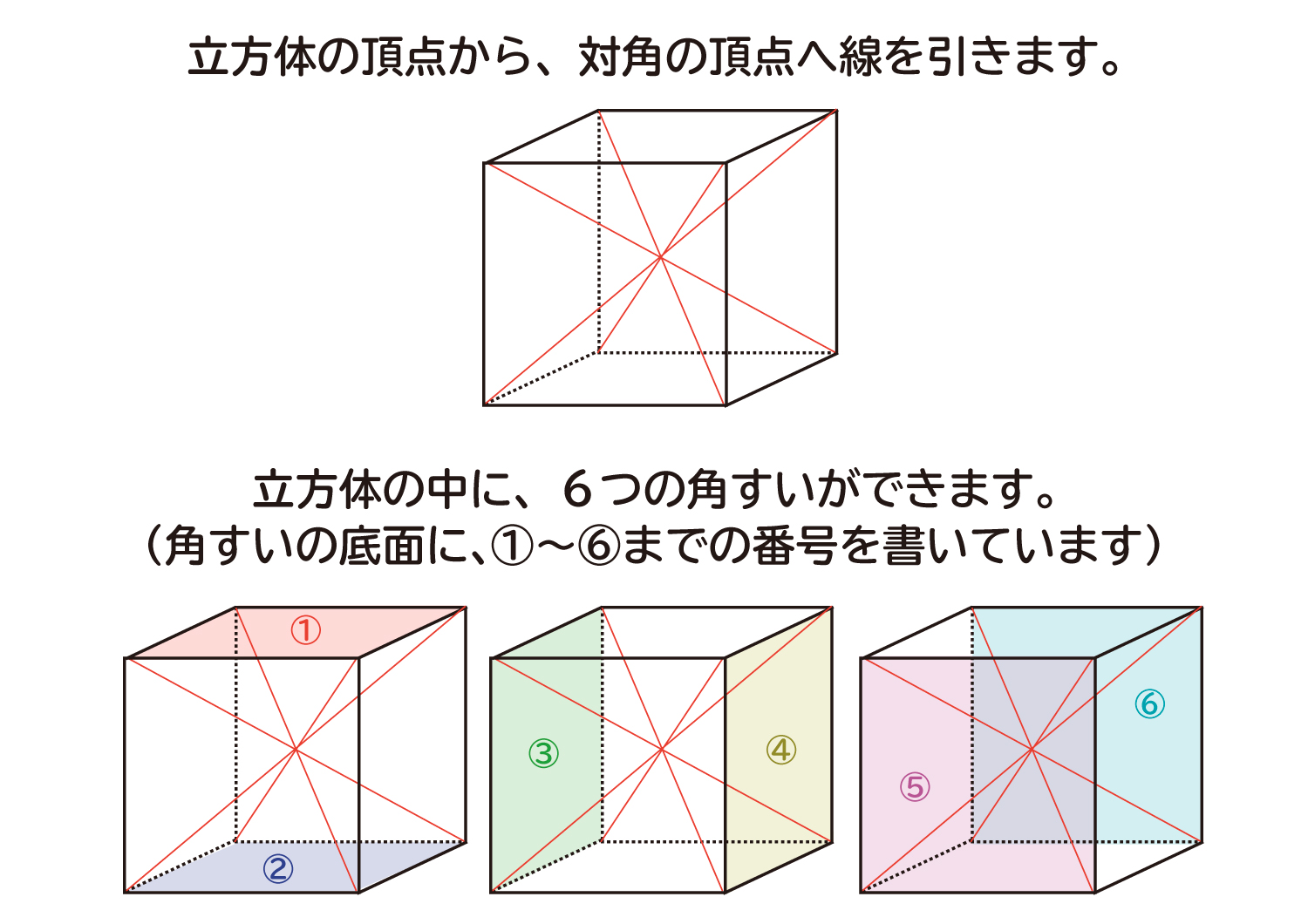
まず、下のような立方体を使って確認します。それぞれの頂点から、対角の頂点へ線を引いてみましょう。すると立方体の中心に向かって、６つの角すいが頂点が重なるようできているのが分かります。（上下に２つ、側面に４つの角すいができています）
次にこの立方体を半分の高さに切った図形では、３つの角すいからできていることになります。つまり、角すいの体積は角柱の１／３ということになります。
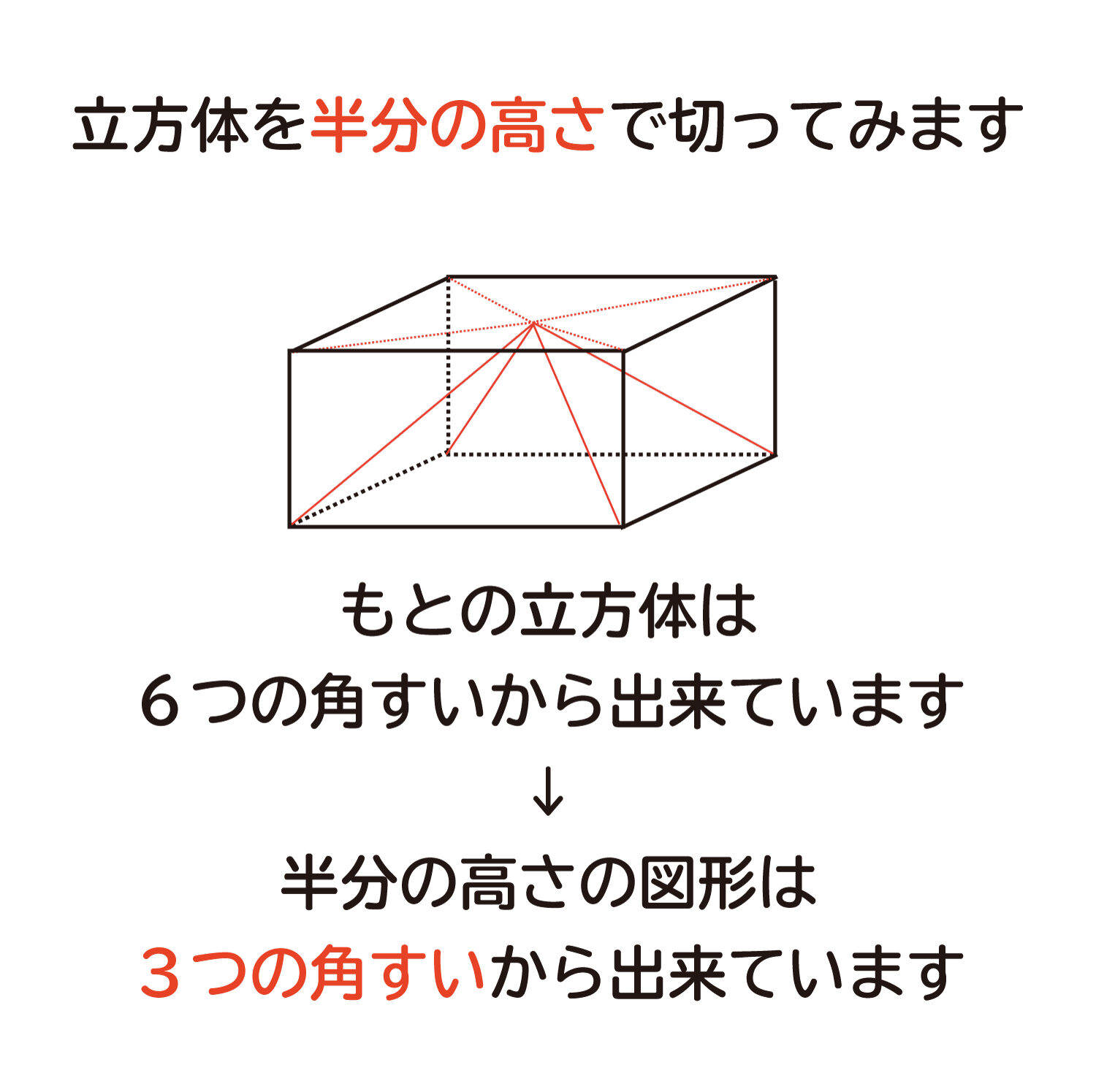
ここで、半分の高さに切った図形は角柱になっており、この角柱の体積は「底面積×高さ」で求めることができます。
そして、この角柱は３つの角すいから出来ているので、角すいの体積はその１／３の「底面積×高さ×１／３」ということになります。
まとめ
・立方体のそれぞれの頂点から、対角の頂点へ線を引くと、６つの角すいを作ることができます。
・この立方体を半分の高さで切った角柱は、３つの角すいからできていることになります。
・そのため、角すいの体積は、角柱の体積の１／３になります。