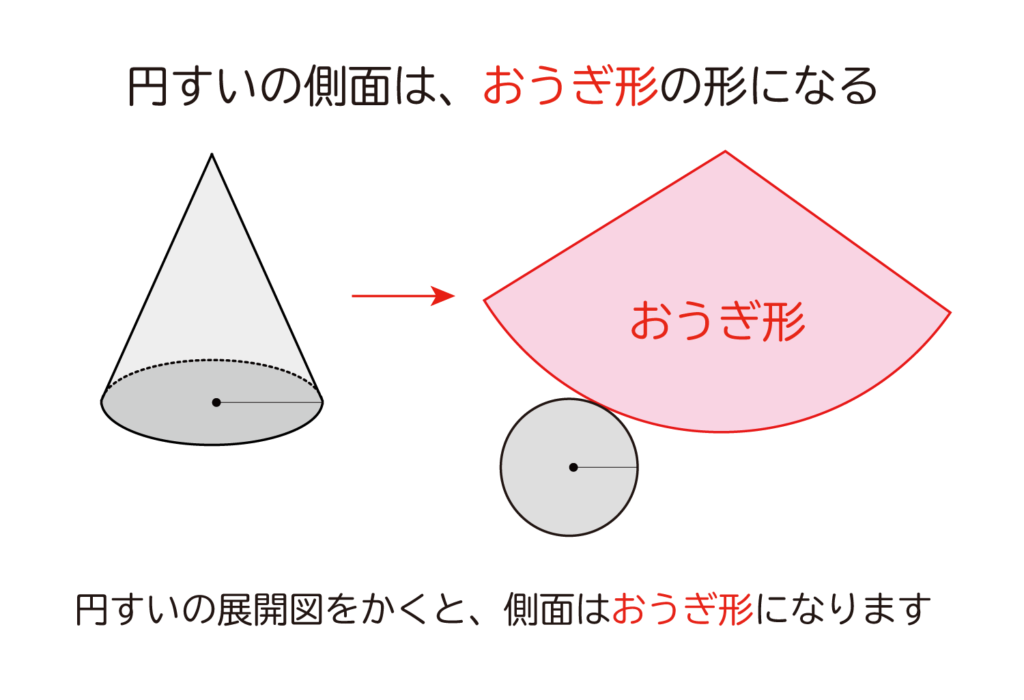
ここではなぜ、円すいの側面は展開すると、おうぎ形になるのか？を考えていきたいと思います。
この公式のポイント
・円すいの側面は、展開するとおうぎ形になります。
円すいの表面積を求める問題を解くには、側面がおうぎ形になっていることを知っておく必要がありますよ
中学生では、円すいの表面積を求める問題が出てきます。
ここでは、円すいの側面がなぜおうぎ形になるのかを考えるときの参考にしてみて下さい。
それでは、さっそく確認していこう！
「円すいの側面の形は、おうぎ形」になる説明
まずはじめに、直角三角形の１辺を中心に１回転させたとき、出来る立体は円すいになります。
この時、円すいの頂点から底面の円周までの長さは、すべて同じ長さ（直角三角形の斜辺と同じ長さ）になっていることが分かります。
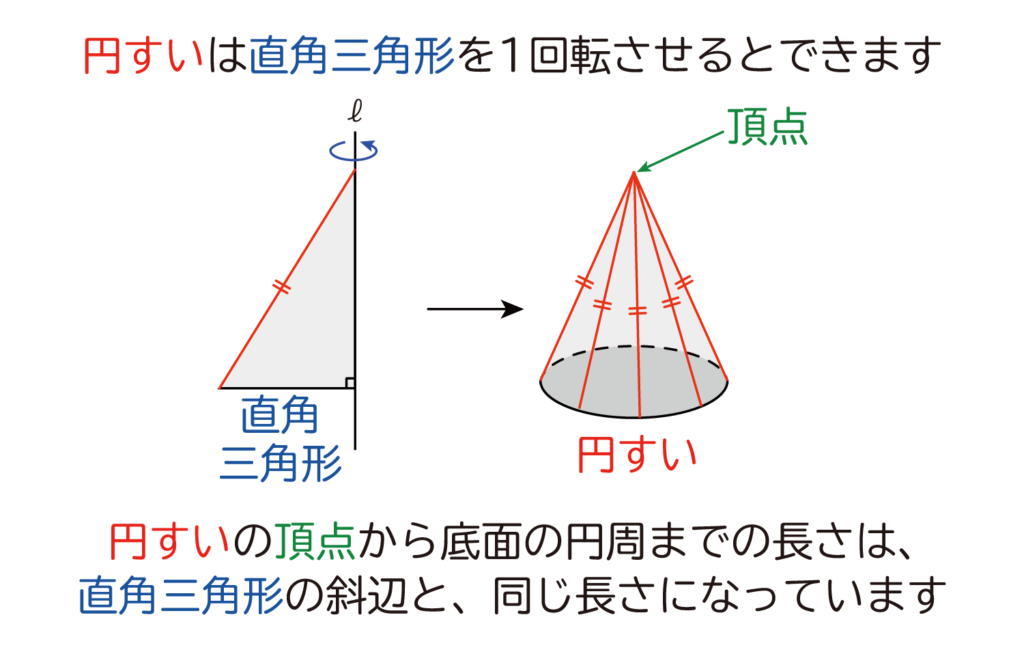
円すいの頂点から、底面の円周に向かう線は、すべて同じ長さになるんだね！
ここで、円の特徴を思い出してみて下さい。
円の中心から円周までの距離は全て等しくなっています。同じようにおうぎ形は円の一部なので、おうぎ形の中心から円周までの距離も全て等しくなっています。
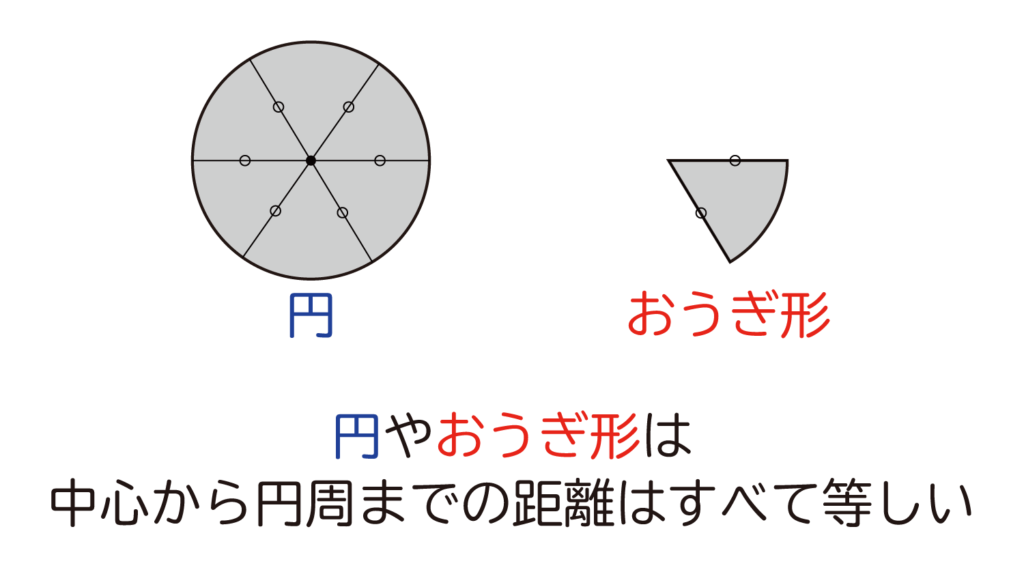
円は円周は、中心から全て等しい距離にあるね！
ここで円すいの頂点から底面の円周までの距離は全て等しいので、円すいの側面の特徴は、円やおうぎ形の特徴と一致しています。
この時、円すいの側面の展開図は円にはならないので、おうぎ形になることが分かります。
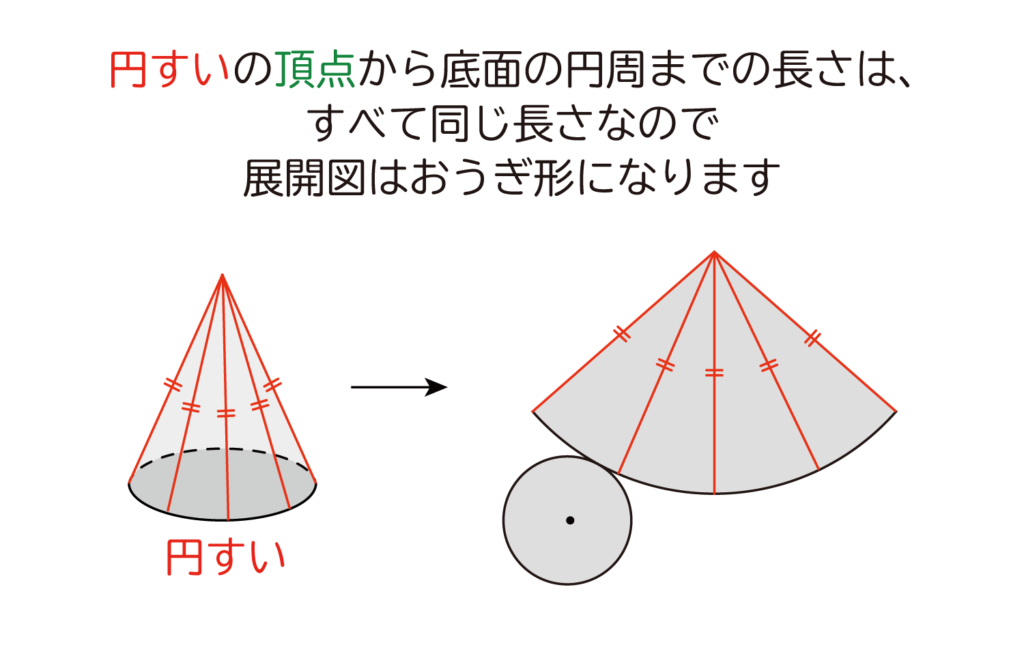
円すいの側面は、おうぎ形になるね！
まとめ
・円すいの頂点から、底面の円周までの距離は全て等しくなっています。
・ある点から全て等しい距離にある図は、円かおうぎ形になります。
・円すいの側面は円にはならないので、おうぎ形になります。
円すいの表面積を求める問題を解く時は、側面がおうぎ形になっていることを思い出してね！
その他の中学生で習う公式は、こちらのリンクにまとめてあるので、気になるところはぜひ読んでみて下さいね。