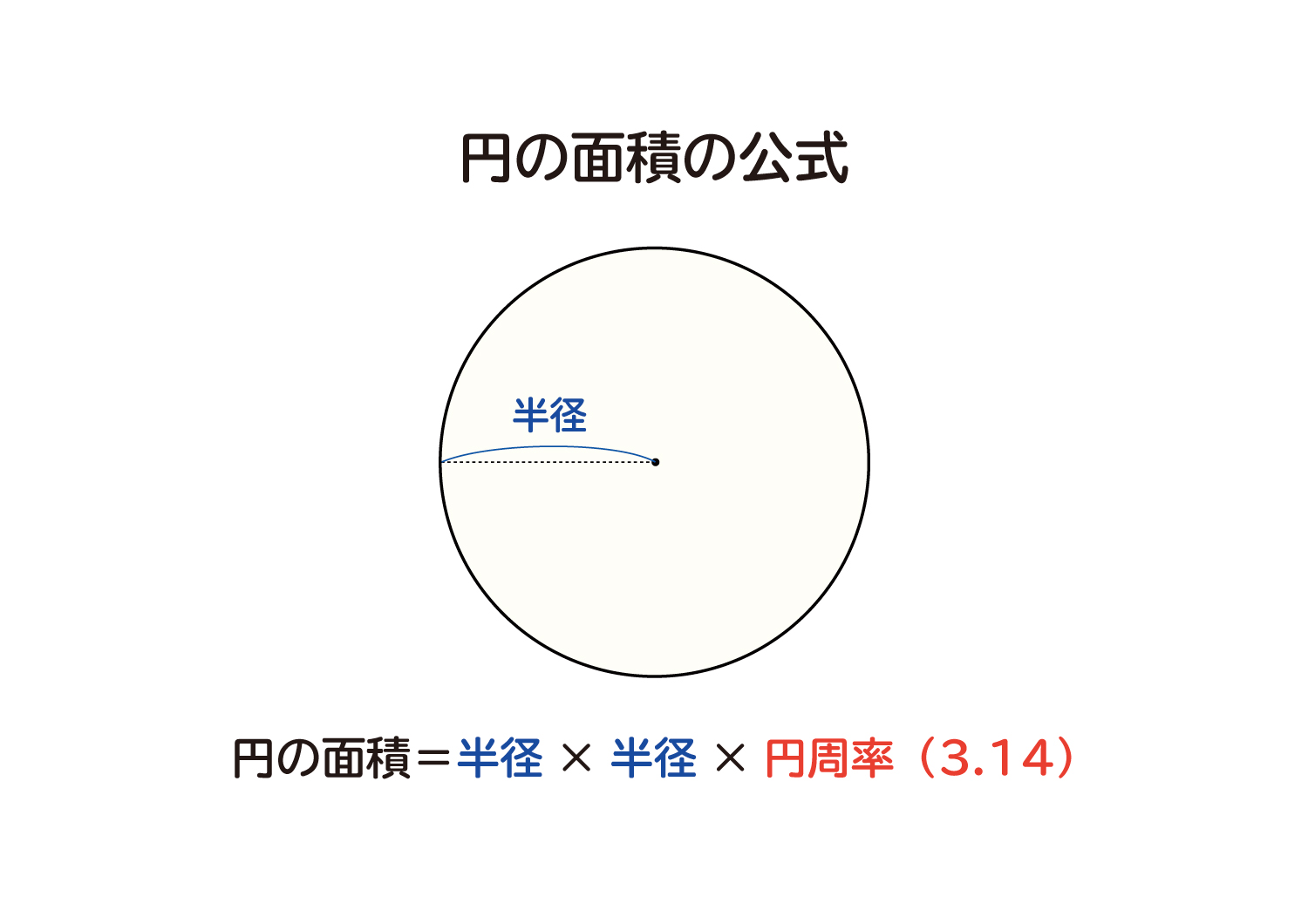
ここでは、なぜ円の面積は「半径×半径×円周率(3.14)」なのか?を、考えていきます。
この公式のポイント
・どんな大きさの円も、面積は「半径×半径×円周率(3.14)」で求めることができます。
円の面積は、なぜこの公式で求められるのか?を考えながら、理解していきたいと思います。
疑問に思ったときに、ぜひ参考にしてみてくださいね。

ぴよ校長
それでは円の面積の公式が、なぜこの式なのか確認してみよう!
円の面積が「半径×半径×円周率(3.14)」になる説明
円の面積の公式を下のような図を使って確認してみたいと思います。
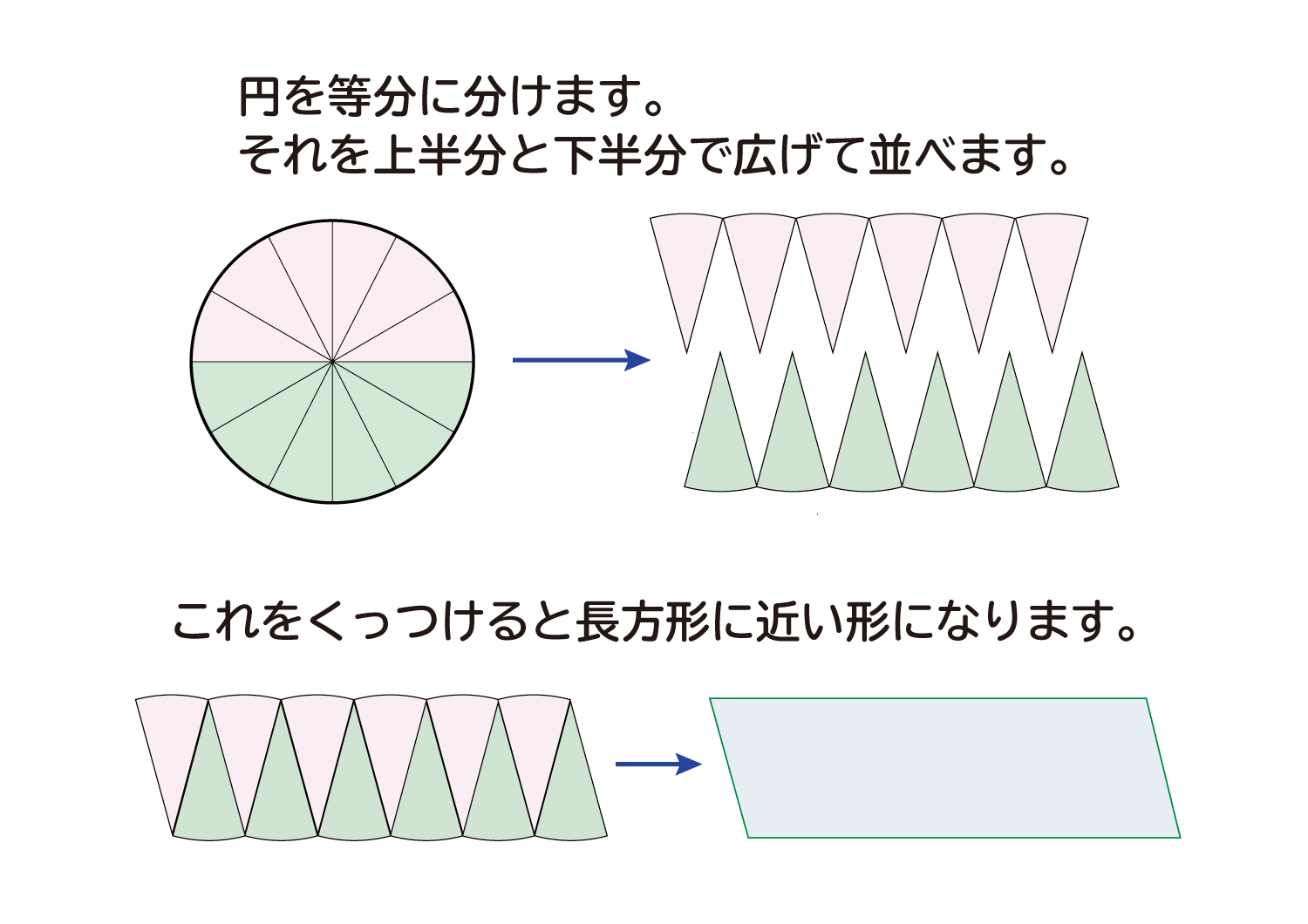
この円を、細かく等分に分けます。そして、等分に分けた上と下を並べると、長方形に近い形になります。
この円を、先ほどよりもっと細かく分けてみると、さっきよりもきれいな長方形の形になってきました。
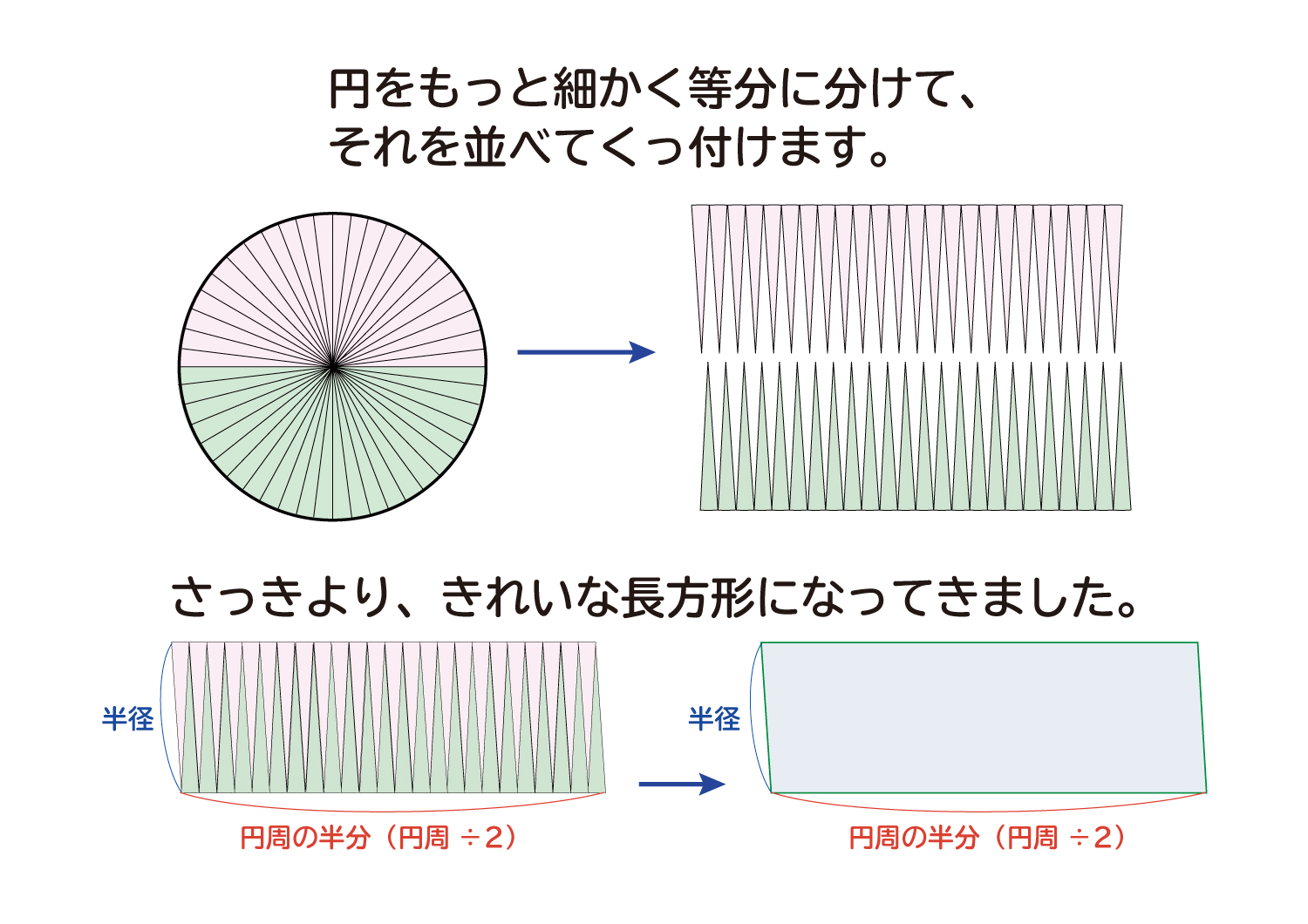
円をどんどん細かく分けていくと、最終的に円は長方形に形を変えることができます。
この円からできた長方形の縦は「半径」と同じ、横は「円周の半分」と同じ長さになっています。
長方形の面積は「縦×横」で求めることができるので、
円から作ったこの長方形の面積は「縦(半径)×横(円周÷2)」になります。

ぴよ校長
円周 = 直径×円周率(3.14)で求められると4年生で勉強したよ!
これをまとめると円の面積は、
半径×円周÷2 = 半径×直径×円周率(3.14)÷2 = 半径×半径×円周率(3.14)
で求めることができます。
まとめ
・円を細かく等分に分けると、長方形に形を変えることができます。
・円で作った長方形の「縦は半径」、「横は円周の半分」と同じ長さです。
・円の面積は「半径×半径×円周率(3.14)」で求めることができます。

ぴよ校長
これで、円の面積の公式も大丈夫だね!
