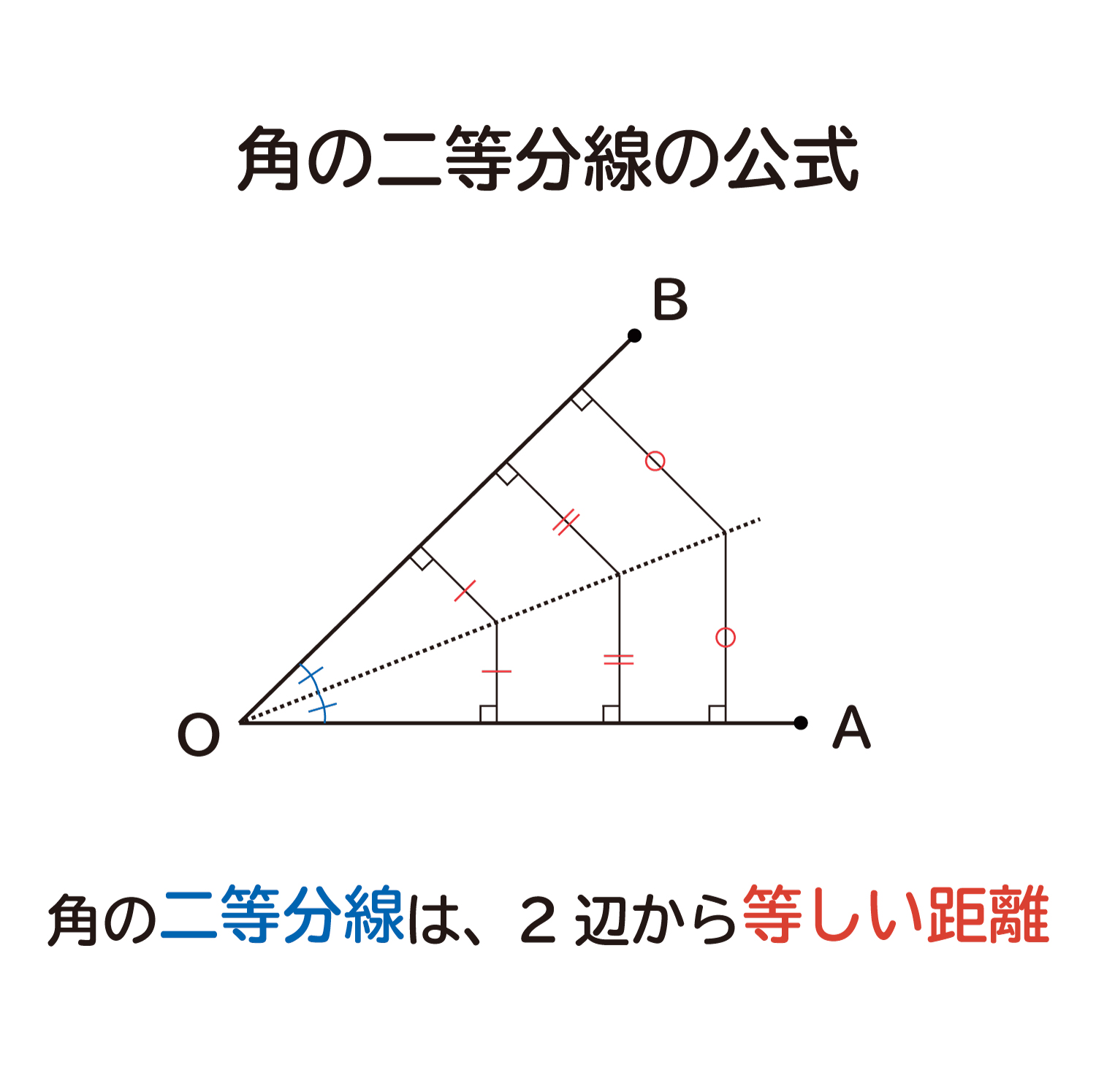
ここでは、なぜ「角の二等分線は、角を作る２辺から等しい距離」なのか？を、考えていきます。
この公式のポイント
・角の二等分線とは、角を2つの等しい角度に分ける直線です。
・その二等分線は、角を作る2辺（辺ＯＡと辺ＯＢ）から等しい距離にあります。
中学1年生では、角の二等分線の公式が出てきます。ここでは図を使って、なぜこの公式が成り立つのか？を考えながら、理解していきたいと思います。
「角の二等分線は、角を作る2辺から等しい距離」になる説明
まず、下の図のように角の二等分線を引き、その上に点Ｐをとります。点Ｐから、辺ＯＡと辺ＯＢのそれぞれに垂線を引き、その交点を点Ｓ、点Ｔとします。
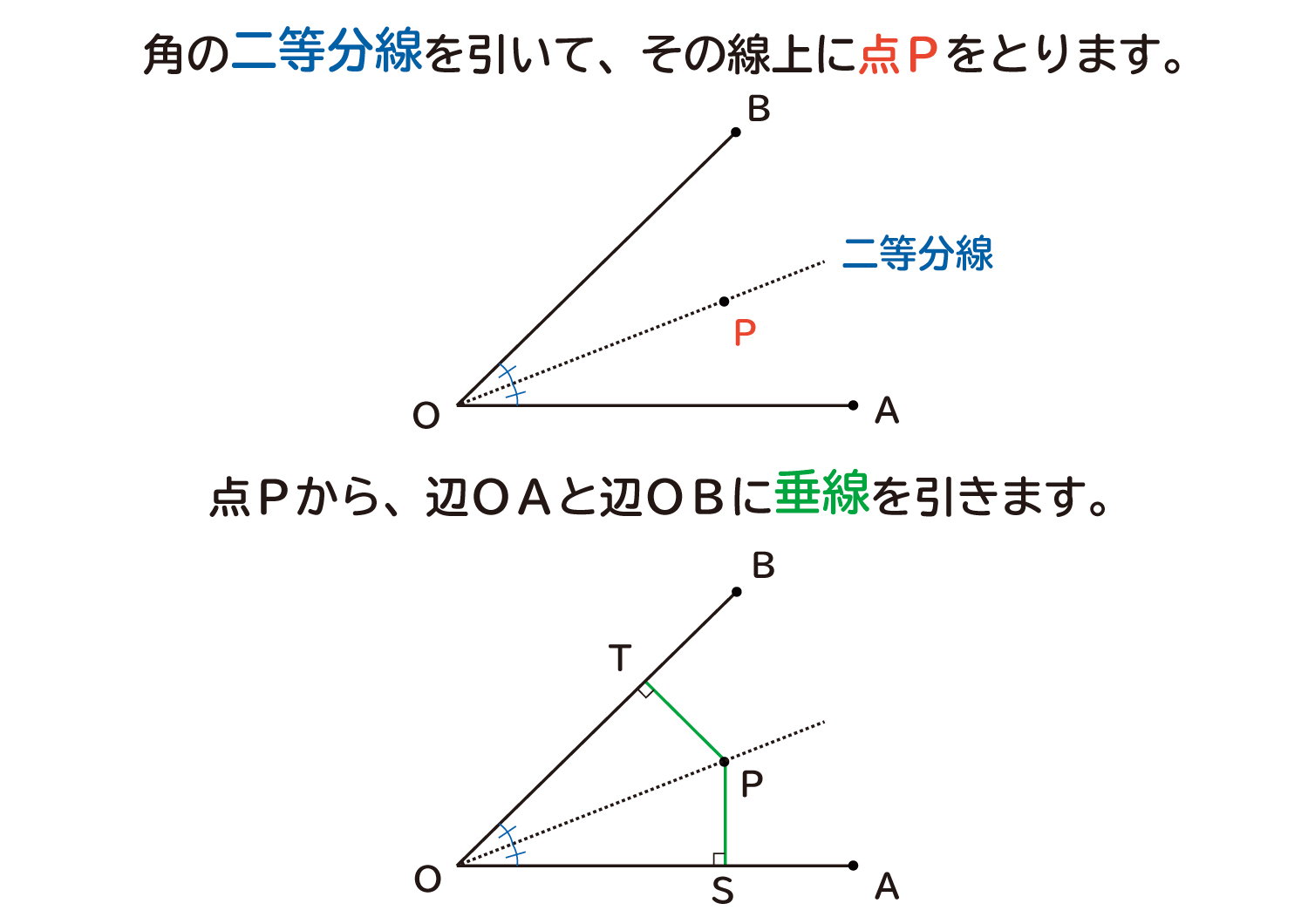
ここで三角形ＳＯＰと三角形ＴＯＰの２つの三角形を考えると、∠ＳＰＯと∠ＴＰＯの２つの角の大きさは、それぞれ下のように計算でき、等しい角になっていることが分かります。
∠ＳＰＯ＝１８０°－９０°－∠ＳＯＰ
∠ＴＰＯ＝１８０°－９０°－∠ＴＯＰ
※直線ＯＰは∠ＡＯＢの二等分線なので、∠ＳＯＰ＝∠ＴＯＰとなっている。
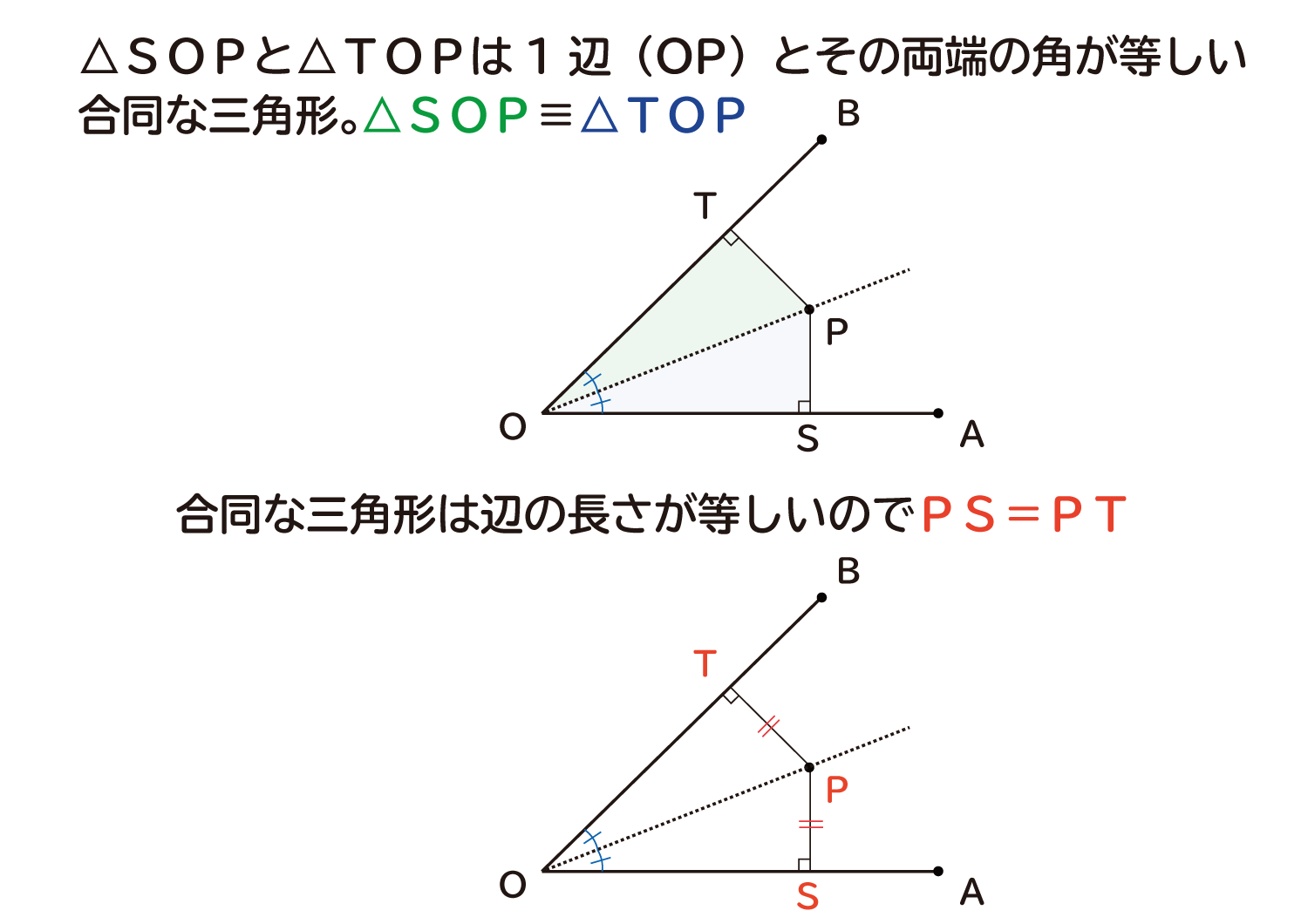
そのため、三角形ＳＯＰと三角形ＴＯＰは、１組の辺（辺ＯＰ）とその両端の角が等しい合同な三角形になっています。△ＳＯＰ≡△ＴＯＰ
合同な三角形は対応する辺の長さは等しいのでＰＳ＝ＰＴとなります。これで点Ｐは辺ＯＡと辺ＯＢから等しい距離にあると確認できました。
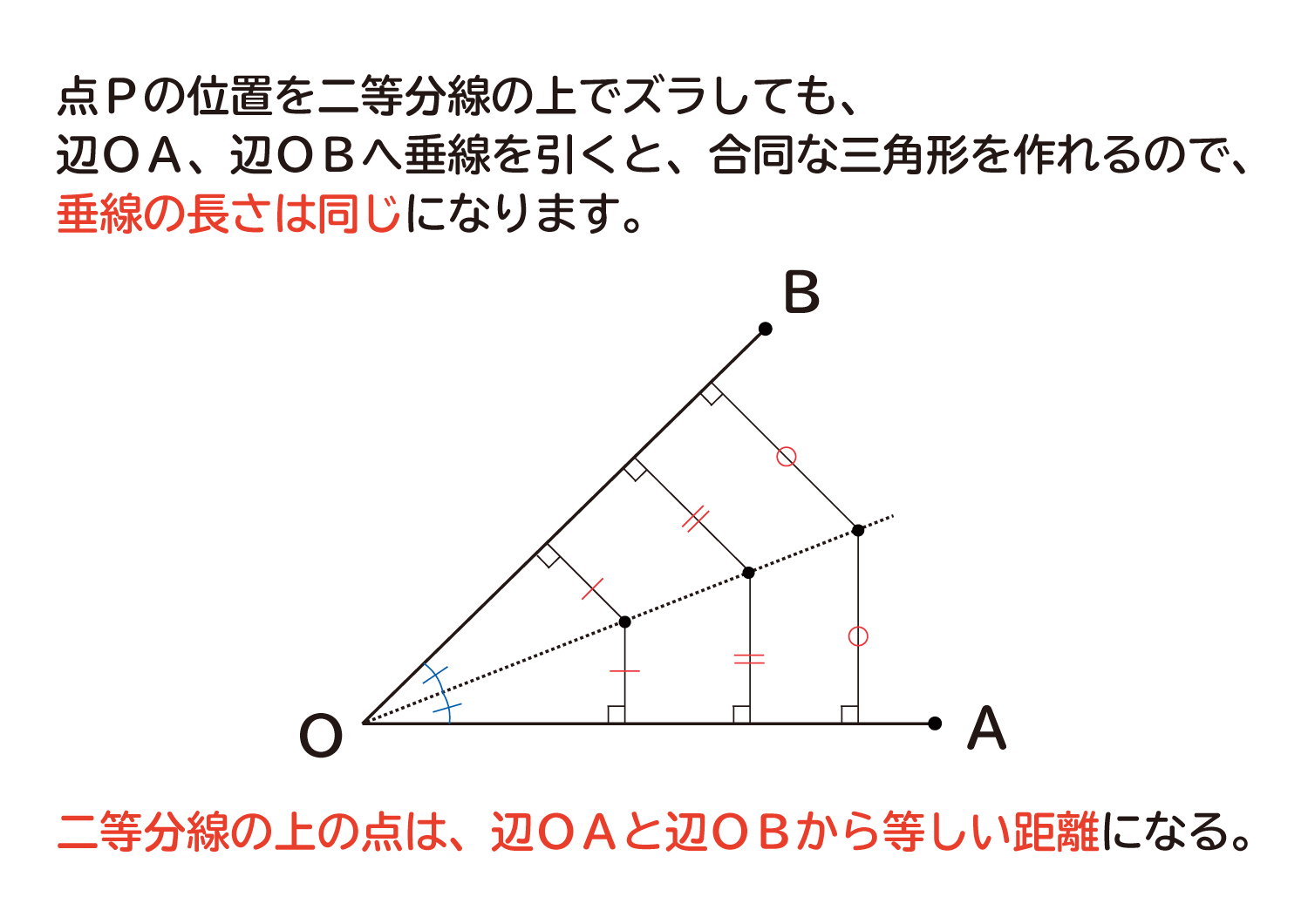
∠ＡＯＢの二等分線の上の点Ｐの位置を、別の場所にズラしてみたときも、それぞれの点から辺ＯＡ、辺ＯＢへ垂線を引くと、合同な三角形を作ることが出来るので、二等分線の上の点は辺ＯＡ、辺ＯＢから等しい距離にあります。
まとめ
・角の二等分線の上の点から、その角を作る２辺へ垂線を引くと、２本の垂線の長さは等しくなります。
・二等分線の上の点の位置をズラしても、２本の垂線の長さは等しくなっています。
・角の二等分線は、その角を作る２辺から等しい距離にあるとわかります。
その他の中学生で習う公式は、こちらのリンクにまとめてあるので、気になるところはぜひ読んでみて下さいね。