 ここでは、多項式同士の掛け算の展開の考え方を説明していきたいと思います。
ここでは、多項式同士の掛け算の展開の考え方を説明していきたいと思います。
中学校では、多項式の展開の公式がいくつか出てきますが、今回は展開公式の意味を理解するための考え方を説明していきたいと思います。
多項式の展開公式を覚える前に、このページでぜひ展開するときの考え方を理解しておきましょう。
多項式の展開のポイント
・多項式同士の展開方法を理解するためには、下のような分配法則を使って考えます。
a(x+y)=ax+ay
(x+y)a=ax+ay

多項式の展開を考えるとき、その基礎となる分配法則を使うことで、展開方法を理解することが出来ます。多項式の展開公式を覚える前に、なぜ展開するときの考え方理解しておくと、もしも公式を忘れてしまった場合にも、問題を解くことに役立ちます。
中学2年生では多項式に整数を掛ける分配法則を使った問題も習っているので、併せてぜひ参考にしてみて下さいね。
参考:多項式に整数を掛ける問題
-
-
中学2年生|数学|多項式と数との乗法
このページは、中学2年生で習う「多項式と数との乗法」が学習できるページです。 こ ...
続きを見る

「多項式同士の掛け算の展開」の考え方
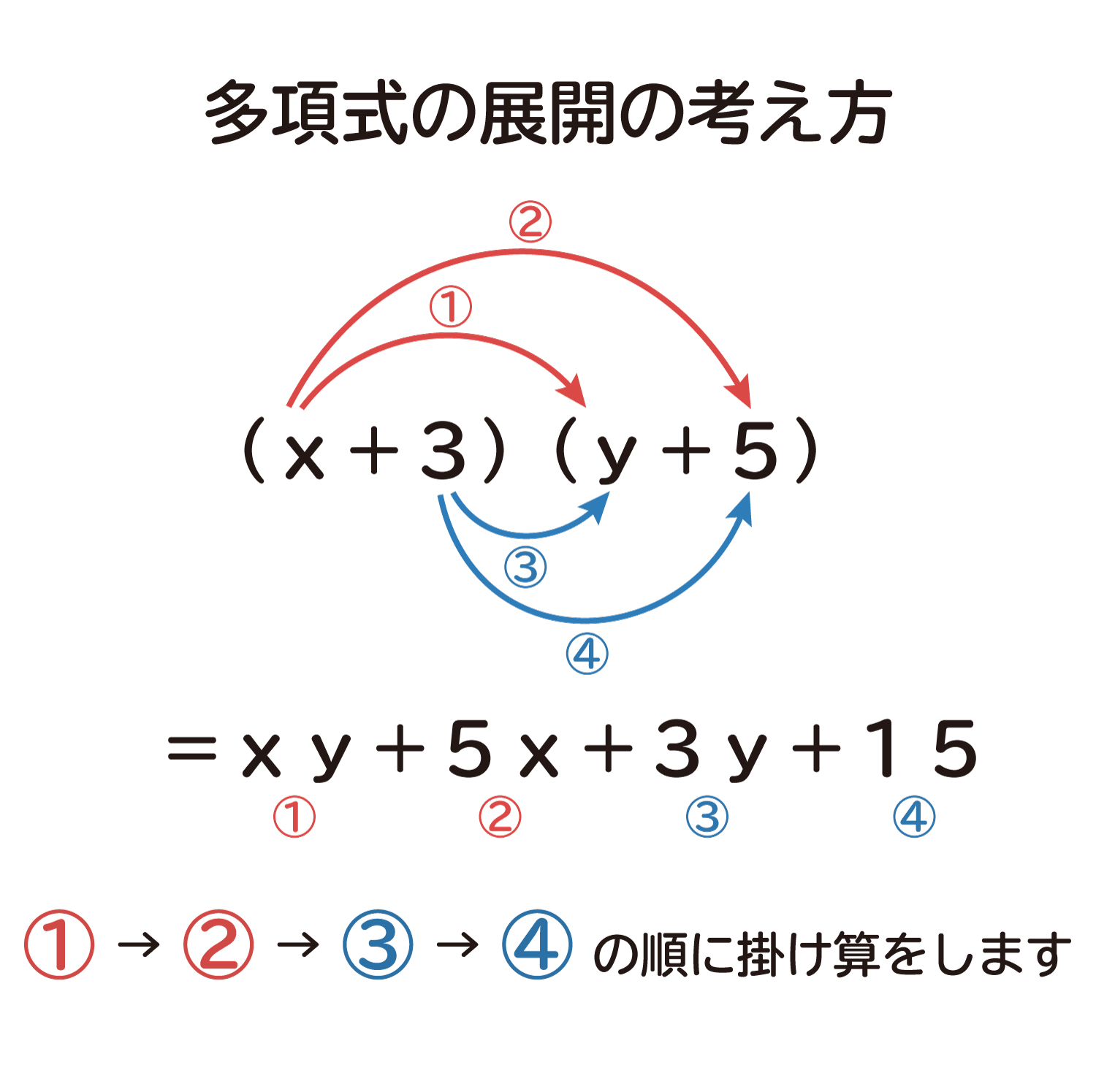
多項式同士の掛け算として、下のような式を考えてみます。
$$\Large(x+3)(y+5)$$
ここで、(y+5)をアルファベット文字「E」として置き換えて考えてみます。
すると、下のような式に書きかえることが出来ます。
$$\Large(x+3){E}$$
この式を分配法則を使って計算すると、下のようになります。
$$\Large(x+3){E}={xE}+{3E}$$

次に、「E」を元の(y+5)の形に戻すと、下のように計算できます。
$$\Large{xE}+{3E}={x}(y+5)+{3}(y+5)$$
この式を、また分配法則で計算してみます。
$$\Large{x}(y+5)={xy}+{5x}$$
$$\Large{3}(y+5)={3y}+{15}$$
上のような分配法則が使えるので、最終的に計算式は、下の形になります。
$$\Large{x}(y+5)+{3}(y+5)={xy}+{5x}+{3y}+{15}$$

これまでの計算をまとめると、多項式同士の掛け算を展開するときは、下の式のように考えれば良いことになります。

まとめ
・多項式同士の掛け算の展開を理解するために、まず1つの多項式を文字などに置き換えて、簡単な形にします。
・次に簡単な形にできた式を、分配法則を使って計算します。
・最後に文字に書き換えた多項式を、元の形に戻して計算すると答えが出せます。

「中学3年生の公式の解説」一覧
