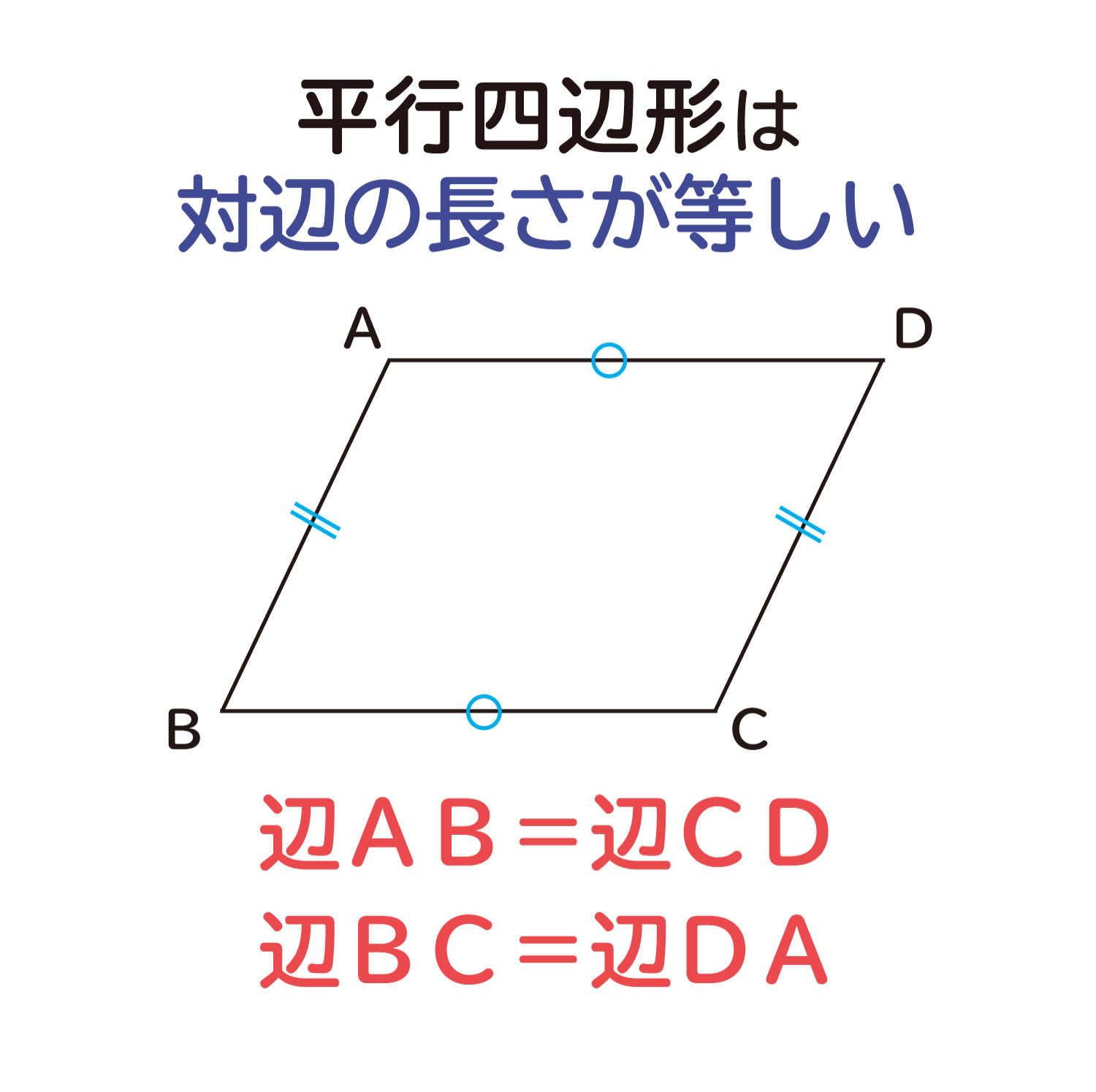
 2組の対辺がそれぞれ平行な四角形を、平行四辺形と定義されます。
2組の対辺がそれぞれ平行な四角形を、平行四辺形と定義されます。
平行四辺形は対辺が平行になっていることでさまざまな性質が現れてきます。そのうちの1つに平行四辺形は、対辺の長さが等しいという性質があります。
ここでは、「平行四辺形の対辺の長さは等しくなる」という性質を確認していきたいと思います。
この公式のポイント
・平行四辺形には、下のような3つの性質があります。
1.対辺の長さが等しい
2.対角の角度が等しい
3.対角線は中点で交わる
今回、1つ目の平行四辺形の性質である、対辺の長さが等しいことを確認していきたいと思います。

平行四辺形は対辺が平行になっていることで、上のような3つの性質が出てきます。これらの性質がそれぞれ正しいことを確認していきましょう。今回はその1つ目の性質の対辺の長さが等しいこと確認していきましょう。
もし、平行四辺形の残り2つの性質についても詳しく知りたい場合は、下のリンクに説明を書いているので、参考にしてみて下さいね。
-
-
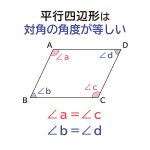
”平行四辺形の対角の角度は等しくなる”ことの説明
2組の対辺がそれぞれ平行な四角形を、平行四辺形と定義されます。 平行四辺形は対辺 ...
続きを見る
-
-
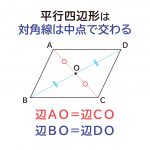
”平行四辺形の対角線は中点で交わる”ことの説明
2組の対辺がそれぞれ平行な四角形を、平行四辺形と定義されます。 平行四辺形は対辺 ...
続きを見る

「平行四辺形は、対辺の長さが等しい」ことの説明
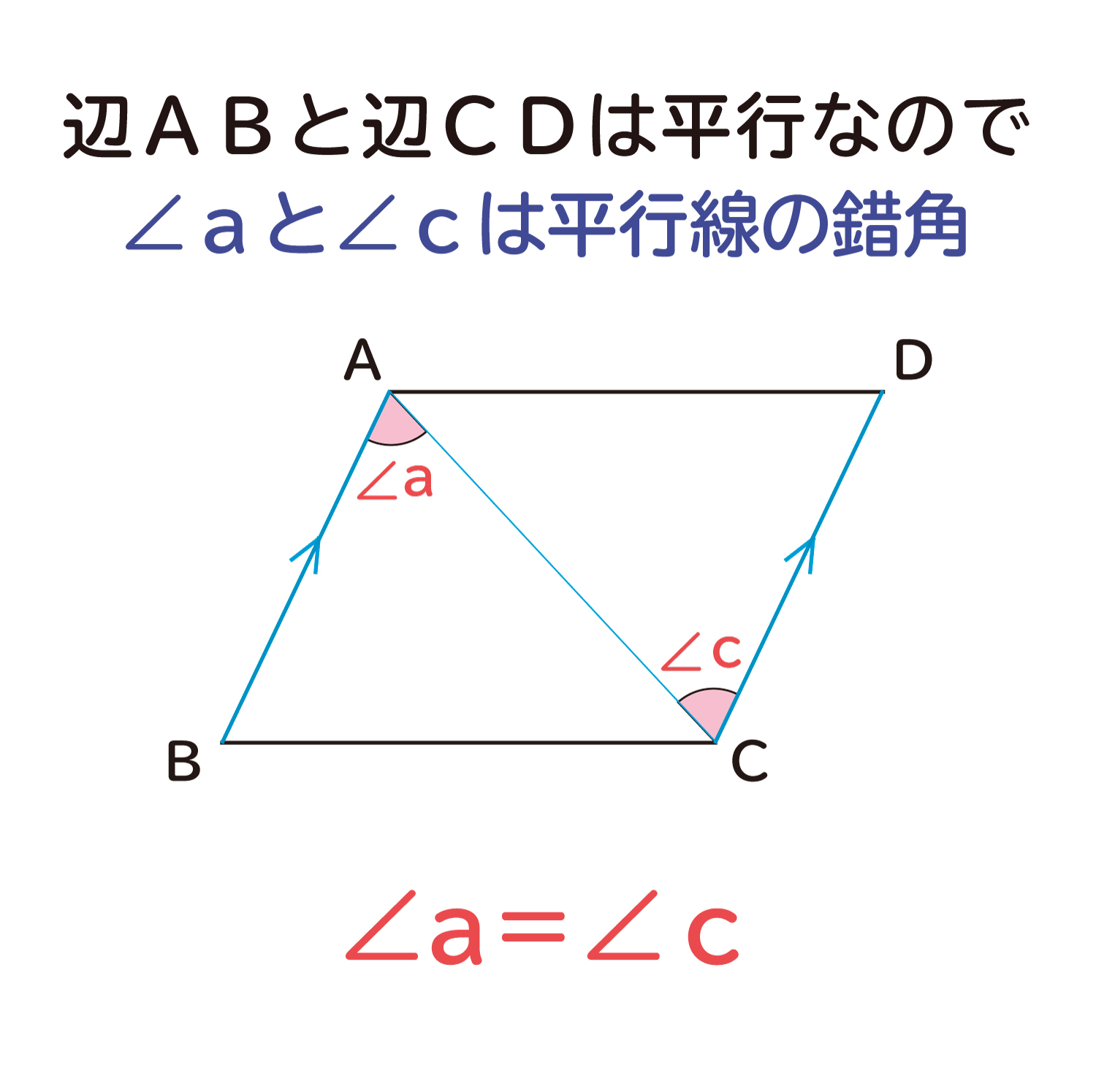
平行四辺形は対辺の長さが等しいことを確認するために、平行四辺形に1本の対角線を引きます。
ここで、辺ABと辺CDは下の図のように平行なので、∠aと∠cは平行線の錯角になります。そして、平行線の錯角は同じ角度になる性質があるので∠a=∠cとなります。
参考:平行四辺形の錯角は等しくなる理由については、下のリンクを参考にしてみて下さいね。
-

-
平行線の同位角と錯角の性質
ここでは中学生の数学で出てくる、平行線の同位角(どういかく)と錯角(さっかく)の ...
続きを見る
次に、辺BCと辺DAも平行になっており、∠xと∠yは平行線の錯角になっています。そのため、∠x=∠yとなります。
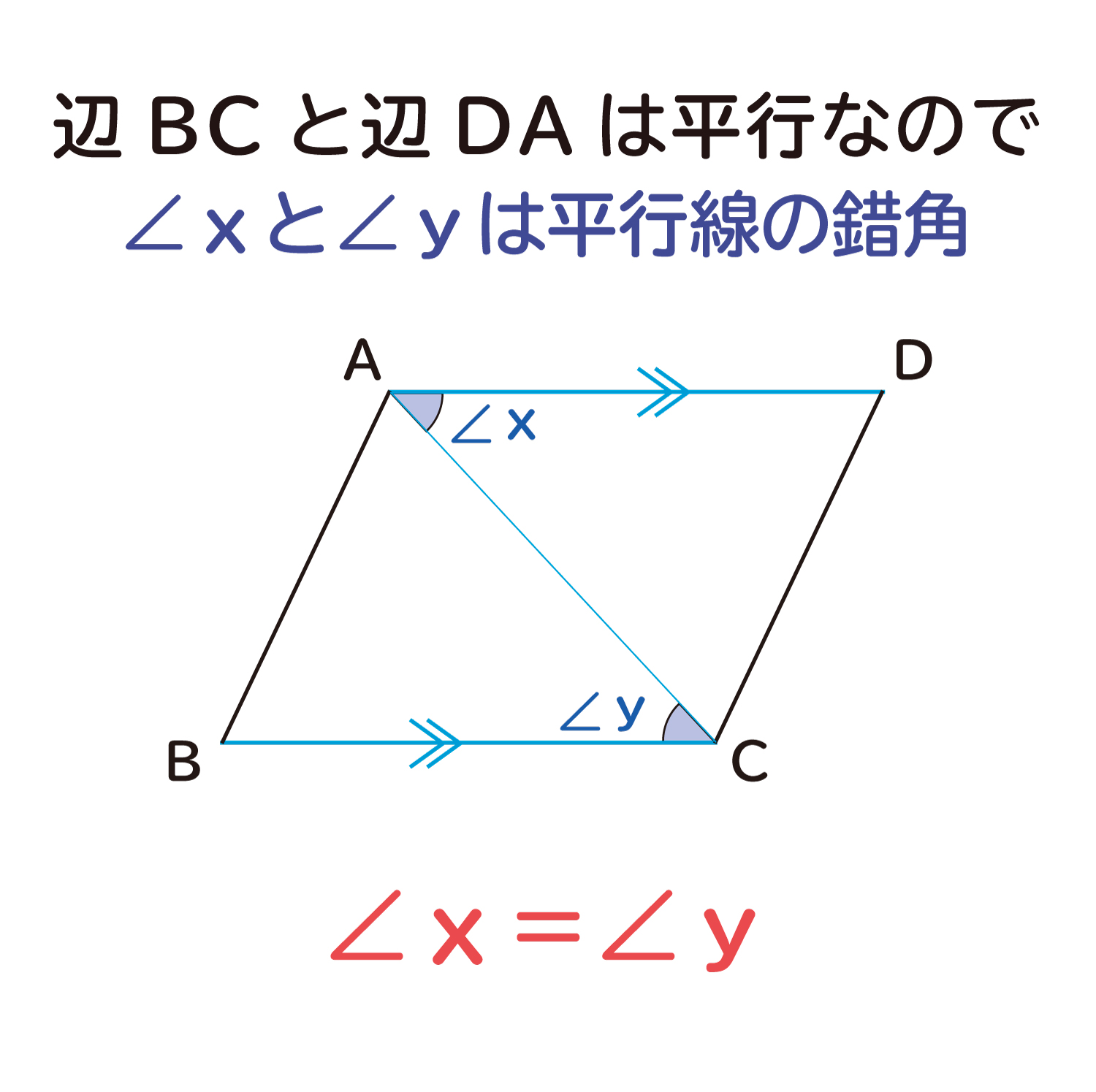
以上のことから、△ABCと△CDAは、辺ACを共通の辺として、1辺のその両端の角の大きさがそれぞれ等しいため、合同な三角形と言えます。
△ABC≡△CDA
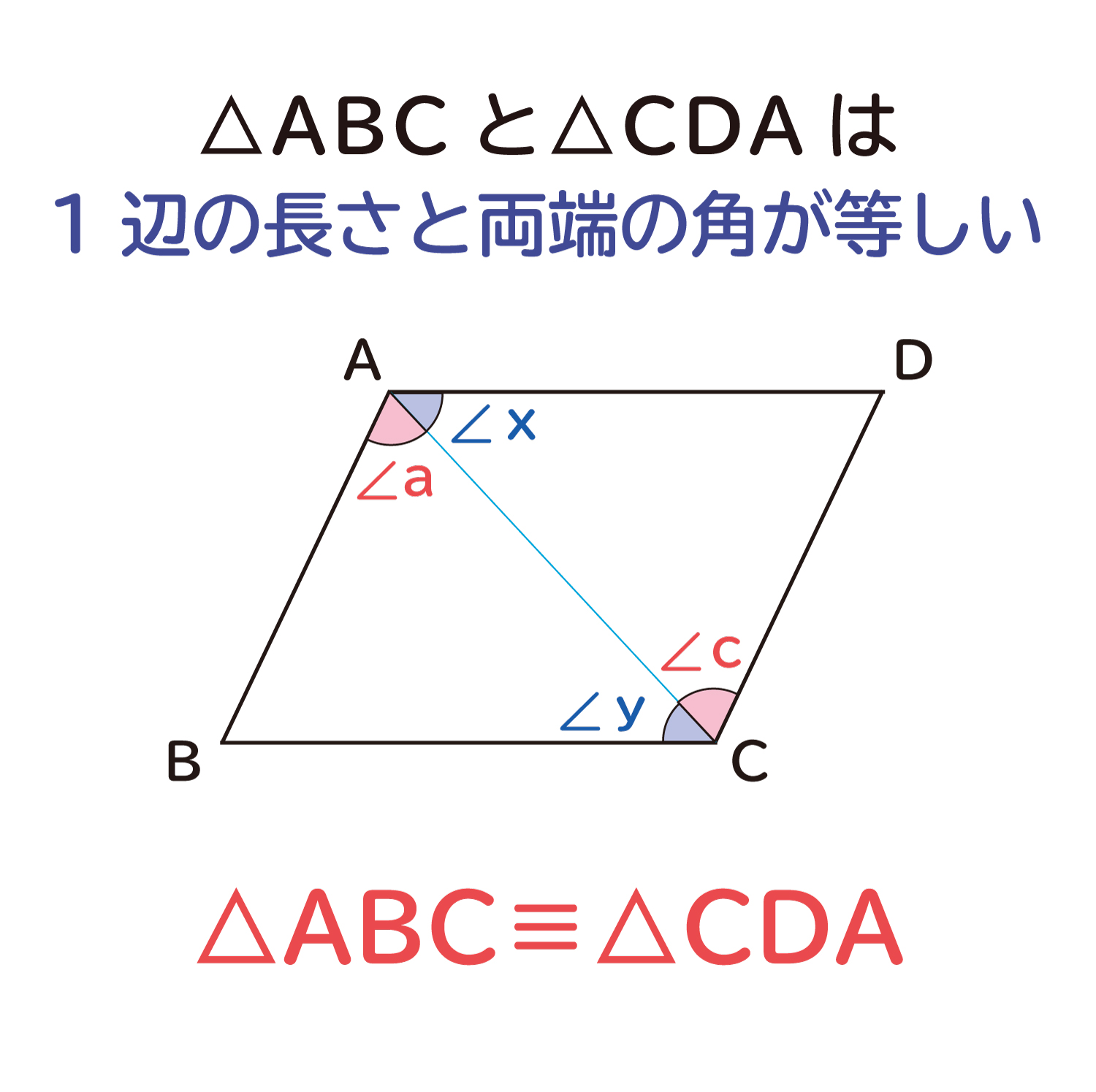
合同な三角形は、それぞれ辺の長さが等しくなるので、辺AB=辺CD、辺BC=辺DAということが言え、平行四辺形の対辺は等しくなることが確認できました!

まとめ
・平行四辺形に対角線を1本引くと、2つの合同な三角形を作ることが出来ます。
・合同な三角形のそれぞれの辺の長さは等しいので、平行四辺形の対辺の長さは等しいと言えます。

「中学2年生の公式の解説」一覧
- 連立方程式の解き方の説明ー代入法を使った解き方ー
- 連立方程式の解き方の説明ー加減法を使った解き方ー
- 直線が交わるときにできる対頂角の性質
- 平行線の同位角と錯角の性質
- 「三角形の1つの外角は、それと隣り合わない2つの内角の和に等しい」ことの説明
- 「n角形の内角の和は、" 180°×(n-2)”」になる説明
- 「n角形の外角の和は 360° 」になる説明
- 三角形の合同条件の説明
- ”二等辺三角形の2つの角は等しくなる”ことの説明
- ”二等辺三角形の頂角の二等分線は、底辺を垂直に二等分する”ことの説明
- ”2つの角が等しい三角形は、二等辺三角形になる”ことの説明
- 直角三角形の合同条件の説明
- ”平行四辺形の対辺の長さは等しくなる”ことの説明
- ”平行四辺形の対角の角度は等しくなる”ことの説明
- ”平行四辺形の対角線は中点で交わる”ことの説明
