連立方程式の解き方の説明ー加減法を使った解き方ー

ここでは、連立方程式の解き方を説明していきたいと思います。上のように、２つの方程式がセットになったものを連立方程式と言います。今回、この連立方程式を加減法という方法を使った解き方で説明したいと思います。

ぴよ校長

方程式に使われている文字を、１つ消せれば解くことが出来るよ！

連立方程式を解くときは、「代入法」と「加減法」の２つの方法のどちらかを使って解くことができます。今回は加減法を使った連立方程式の解き方の説明をしていきたいと思います。

ぴよ校長

それでは、連立方程式を加減法を使って解く方法を確認していこう！

「連立方程式の解き方ー加減法を使った解き方ー」の説明

連立方程式の解き方の確認として、下の式を考えます。

ここで、（１）の式と、（２）の式のｘの係数に注目すると、等しい（両方ともに１）値になっています。そこで（１）の式から（２）の式を引くと、ｘを消すことができます。引き算の計算を書いてみると、下のような式になります。

ぴよ校長

（１）の式から、（２）の式を引くと、式の中の文字は「ｙ」だけになったね！

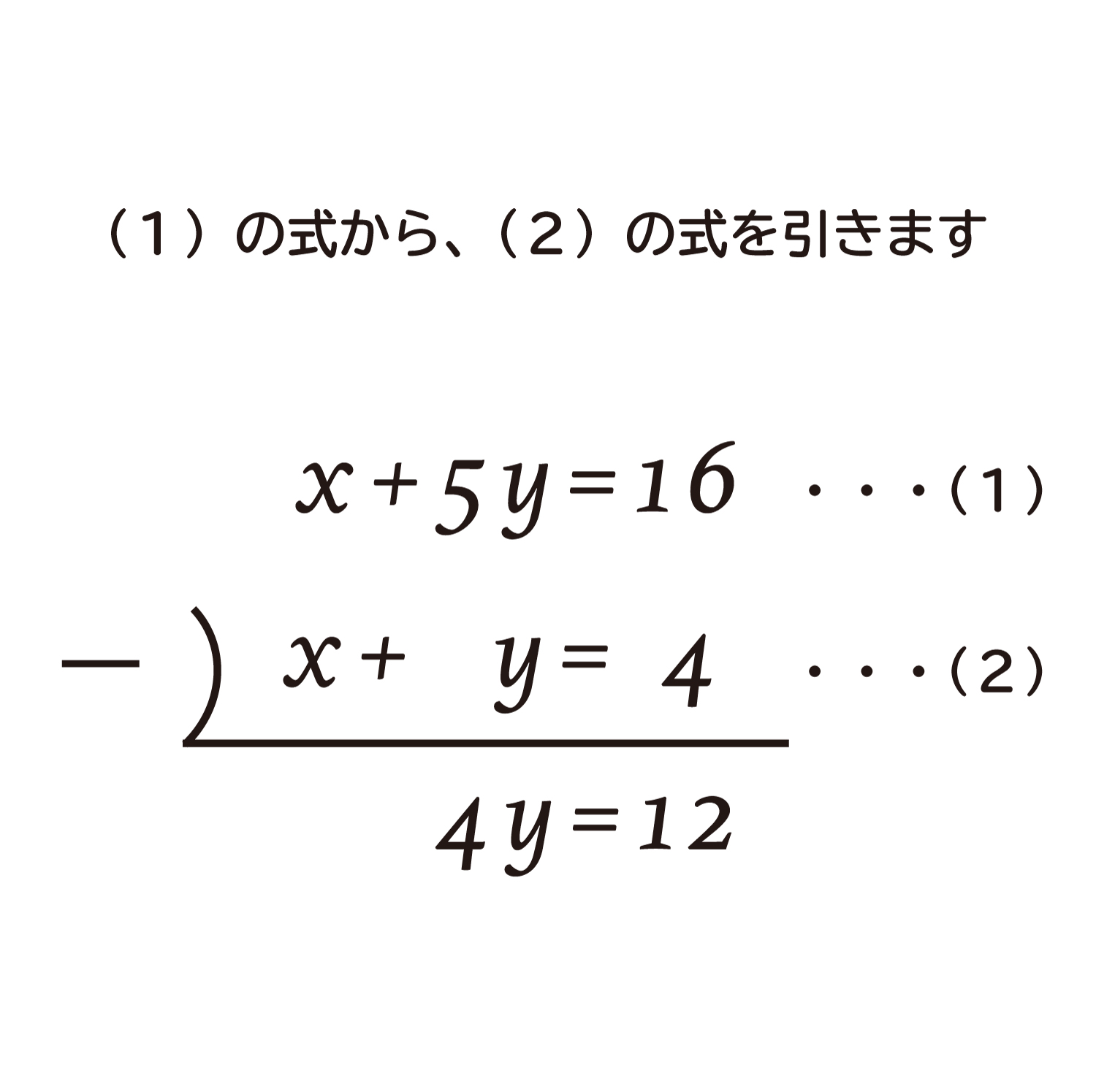
これで、ｙだけになった式から、ｙの値を求めることができます。

$$\Large{4y}={12}$$

$$\Large{y}={3}$$

ここで求めたｙの値を、次に（２）の式の中のｙに入れてみます。ｙ＝３を（２）の式に代入すると

$$\Large{x}＋{y}={4}$$

ｙ＝３を代入して

$$\Large{x}＋{3}={4}$$

$$\Large{x}={1}$$

これで、ｘの値も求めることが出来ました。

ぴよ校長

ｘとｙ、両方の値を求めることが出来たね！

このように、連立方程式では２つの文字（ｘやｙ）のうち、どちらか１つの文字を消すことが出来れば、文字の値を求めることができます。連立方程式の問題を解くときは、今のように１つの式からもう１つの式を、足したり、引いたりする加減法という方法か、これとは別の方法として式を代入する代入法で解くことができます。

代入法での解き方については、下のリンクに説明を書いているので、ぜひ参考にしてみて下さいね。

ぴよ校長

連立方程式を解くときの参考にしてみて下さいね！