
ここでは、多角形の内角の和は何度なのか?を、考えていきます。
上の図に少し説明を書いていますが、多角形は角が1つ増えるごとに、内角の和は180°ずつ増えていきます。
この公式のポイント
・多角形は、三角形から角が1つ増えるごとに、内角の和は180°ずつ増えます。
・多角形の内角の和を出すためには、三角形の内角の和は180°の公式を使います。
なぜ多角形は角が1つ増えるごとに、内角の和は180°ずつ増えるのか?を考えながら、多角形の内角の和の公式を理解していきたいと思います。
多角形の内角の和について、疑問に思ったときやお子さんから質問されたときに、ぜひ参考にしてみてくださいね。
「多角形の内角の和」を理解する上で、「三角形の内角の和は180°」という公式が重要になります。

もし「三角形の内角の和は、なぜ180°なのかな?」という疑問が出てきた時には、先にこちらのリンクから内容を確認してみて下さいね。
-
-
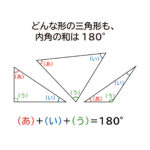
「三角形の内角の和が180°」になる説明
ここでは、なぜ三角形の内角の和は180°なのか?を考えていきます。 この公式のポ ...
続きを見る

多角形の内角の和は何度か?の説明
多角形では、三角形から角が1つ増えるごとに、内角の和が180°ずつ増えていきます。
まずは三角形より角が1つだけ多い四角形について、内角の和を考えてみましょう。

下の図のように四角形の1つの頂点から、別の頂点へ1本の線を引いてみます。
すると四角形を、2つの三角形に分けることができます。
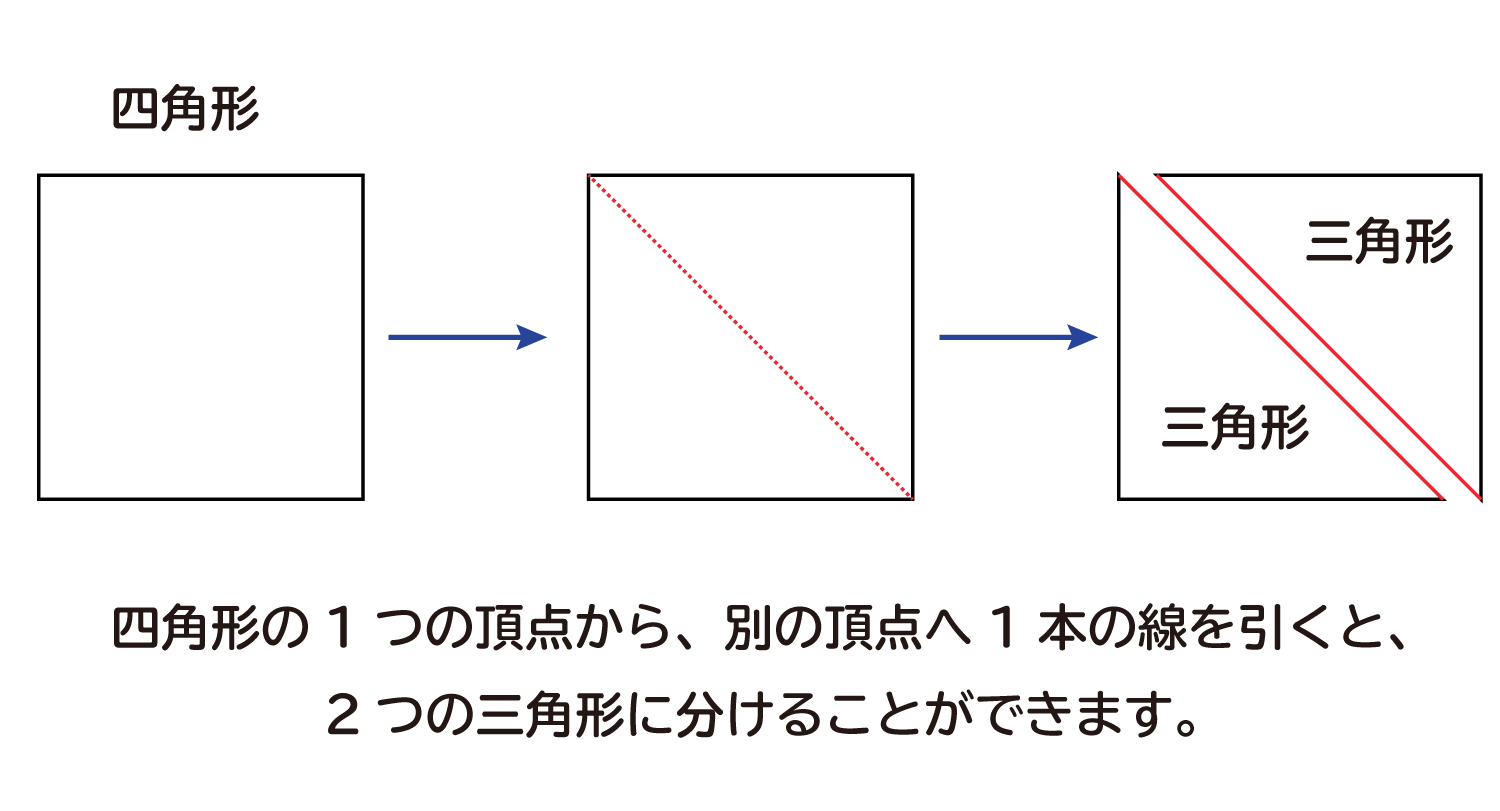
三角形の内角の和は180°なので、2つの三角形からできている四角形では、内角の和は180°×2=360°になります。

上では、正方形の四角形で考えてみましたが、少し変わった形の四角形ではどうでしょうか?

下の図のように、凹んだ部分があるような四角形でも、ちゃんと2つの三角形に分けることができます。
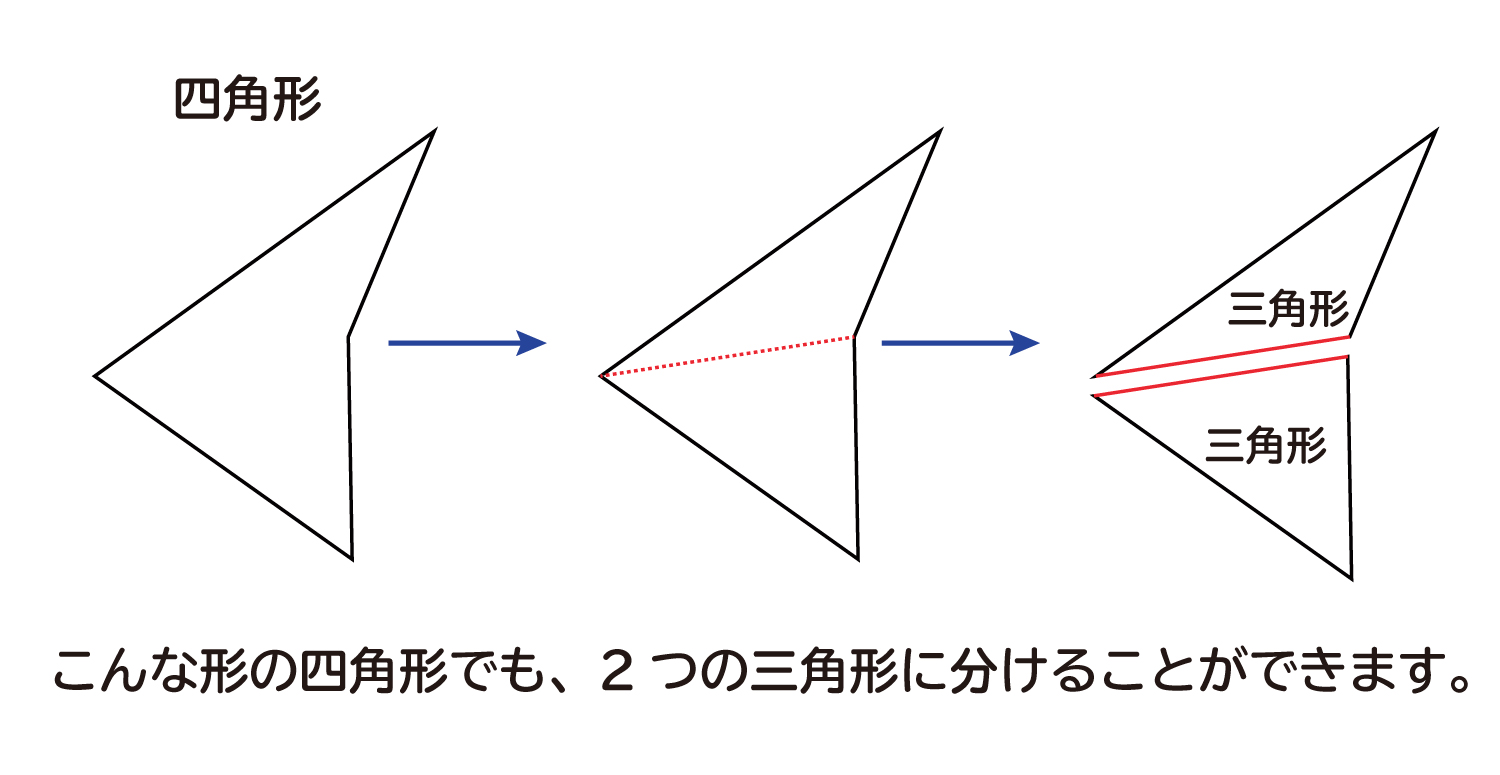
四角形の内角の和のポイント
・四角形は、2つの三角形に分けることができます。
・四角形の内角の和は、三角形2つ分の内角の和なので、180°×2=360°となります。
次は、五角形の内角の和を考えてみます。
四角形と同じように、下の図のような正五角形と、少し変わった形の五角形を見てみます。
五角形は頂点からそれぞれの頂点へ線を引くと、3つの三角形に分けることができます。
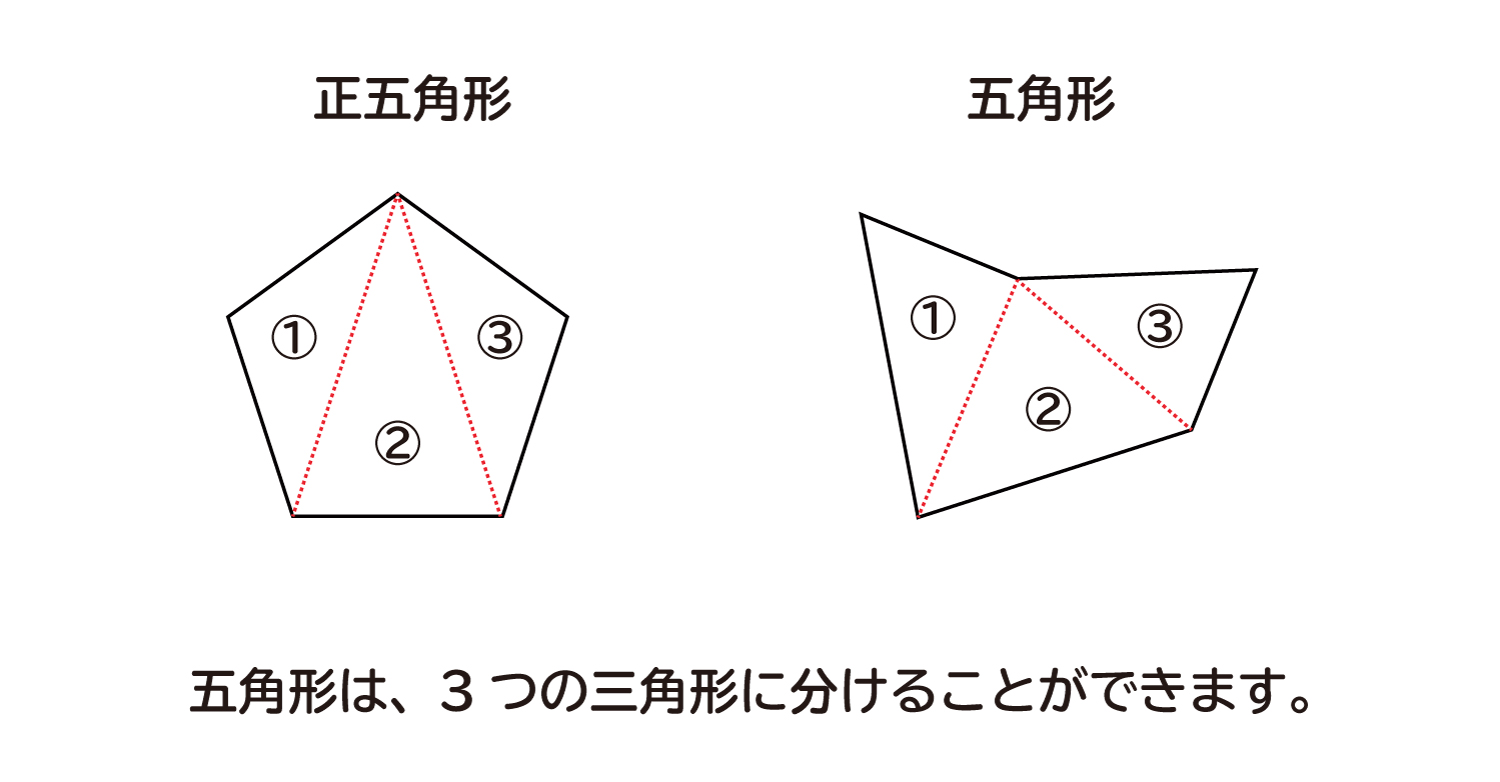
五角形は3つの三角形からできているので、内角の和は180°×3=540°になります。
五角形より角の多い多角形でも、角が1つ増えるごとに、分けられる三角形の数は1つずつ増えていきます。

これを式にしてまとめると、「n角形の内角の和は180°×(n-2)」となります。

例)九角形の場合は、n=9なので、九角形の内角の和は180°×(9-2)=180°×7=1260°
まとめ
・多角形は角が1つ増えるごとに、内角の和は180°ずつ増えます。
・n角形の内角の和は、180°×(n-2)となります。

