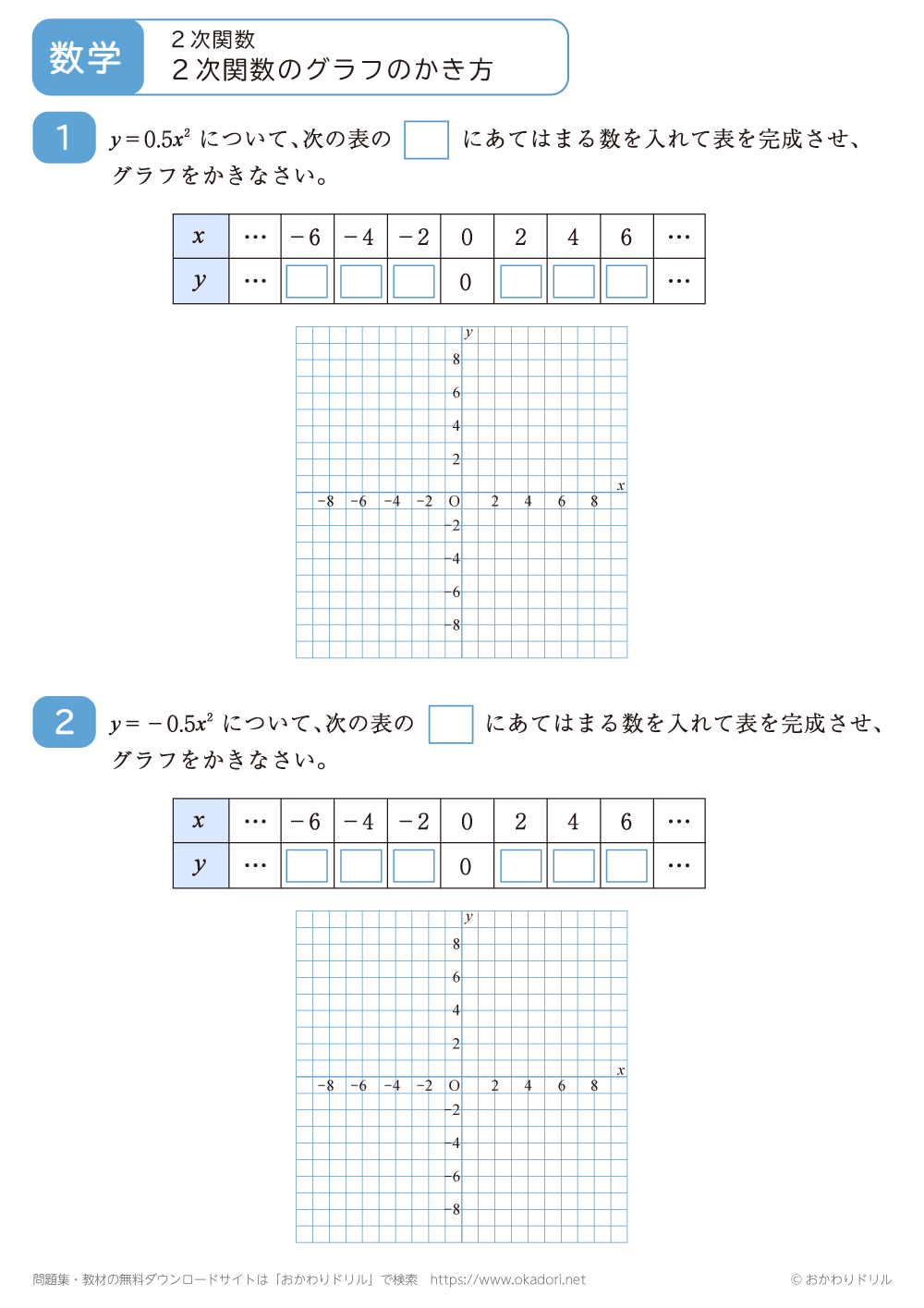
このページは、中学3年生で習う「2次関数のグラフのかき方」が学習できるページです。
この問題のポイント
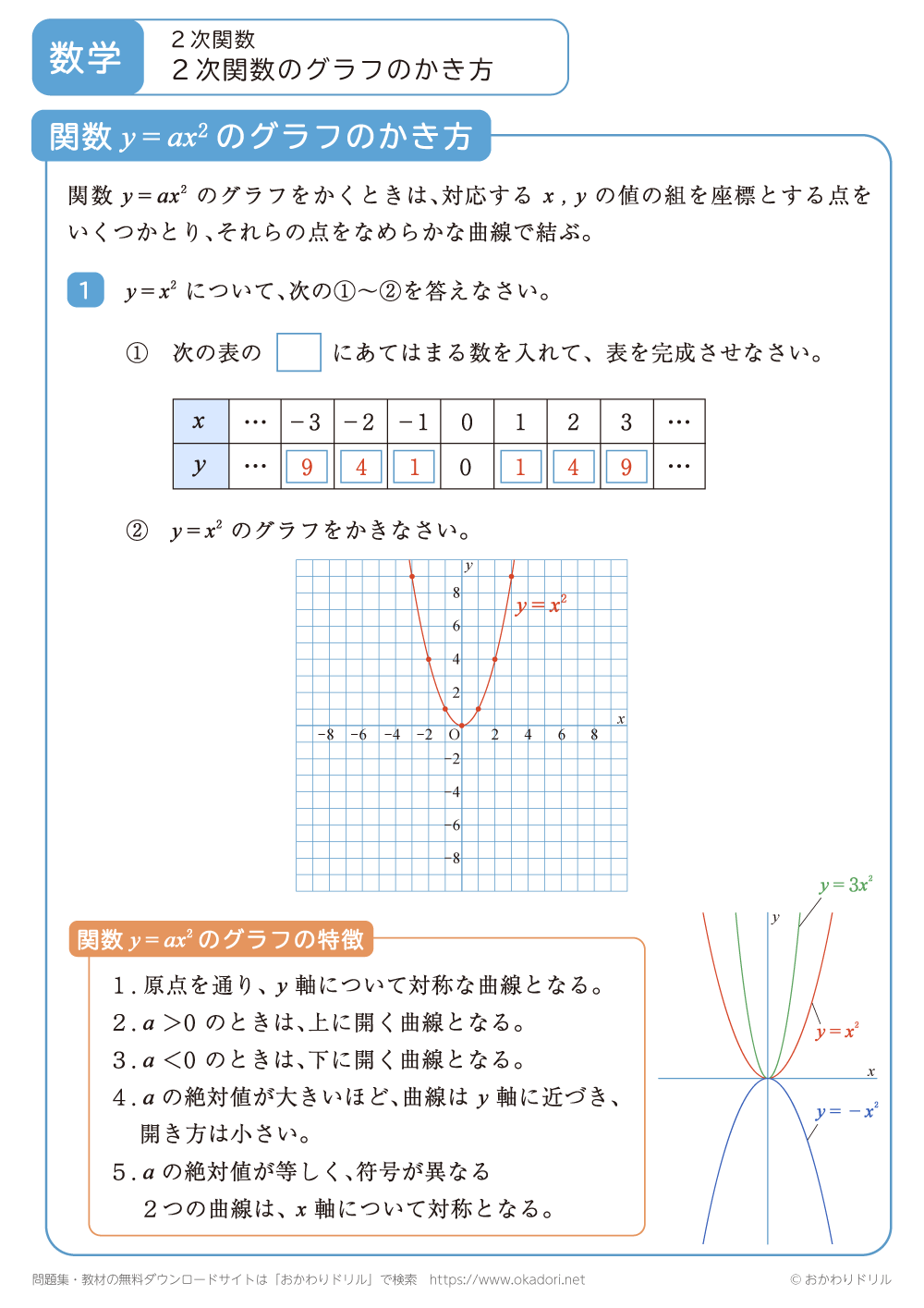
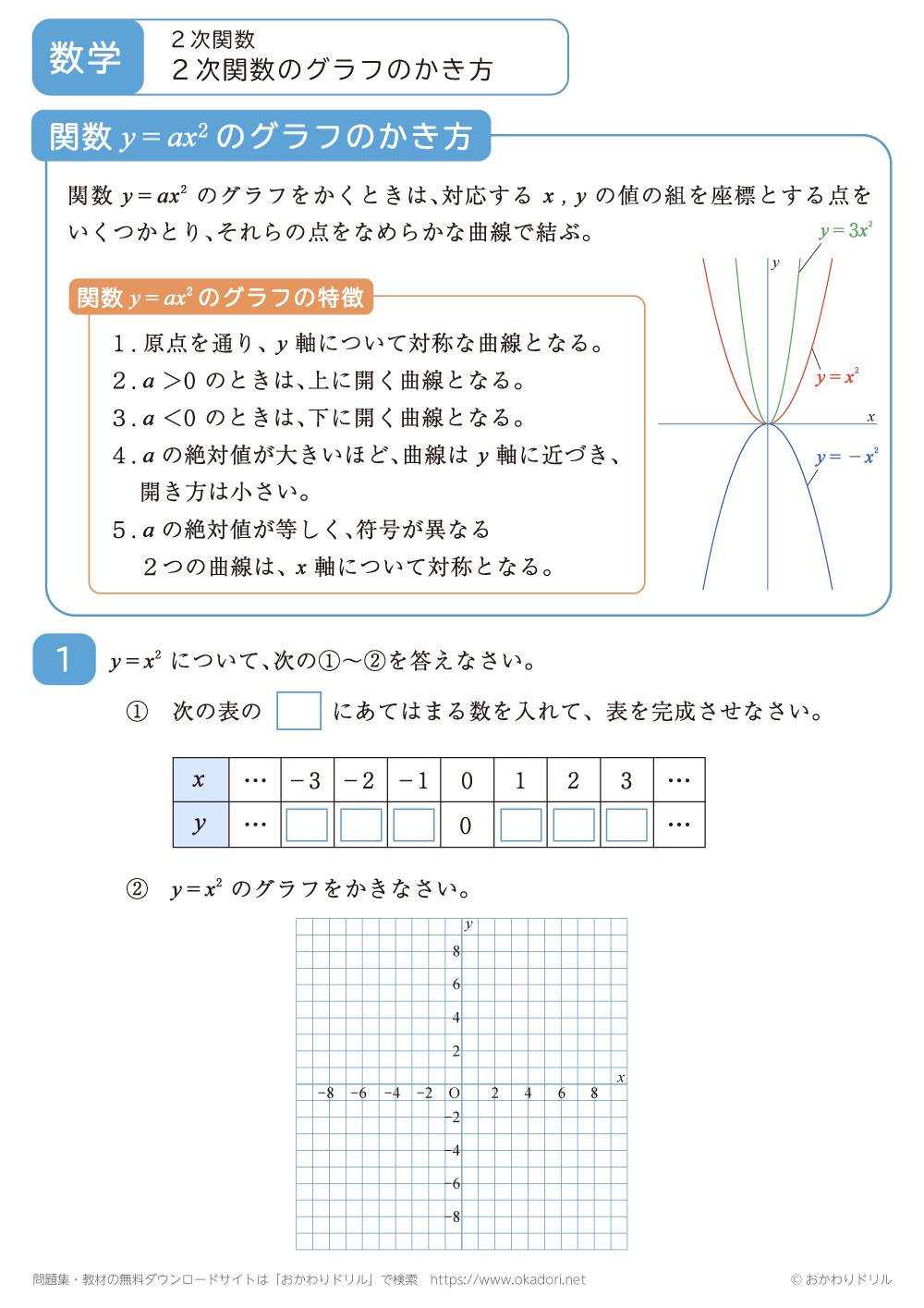
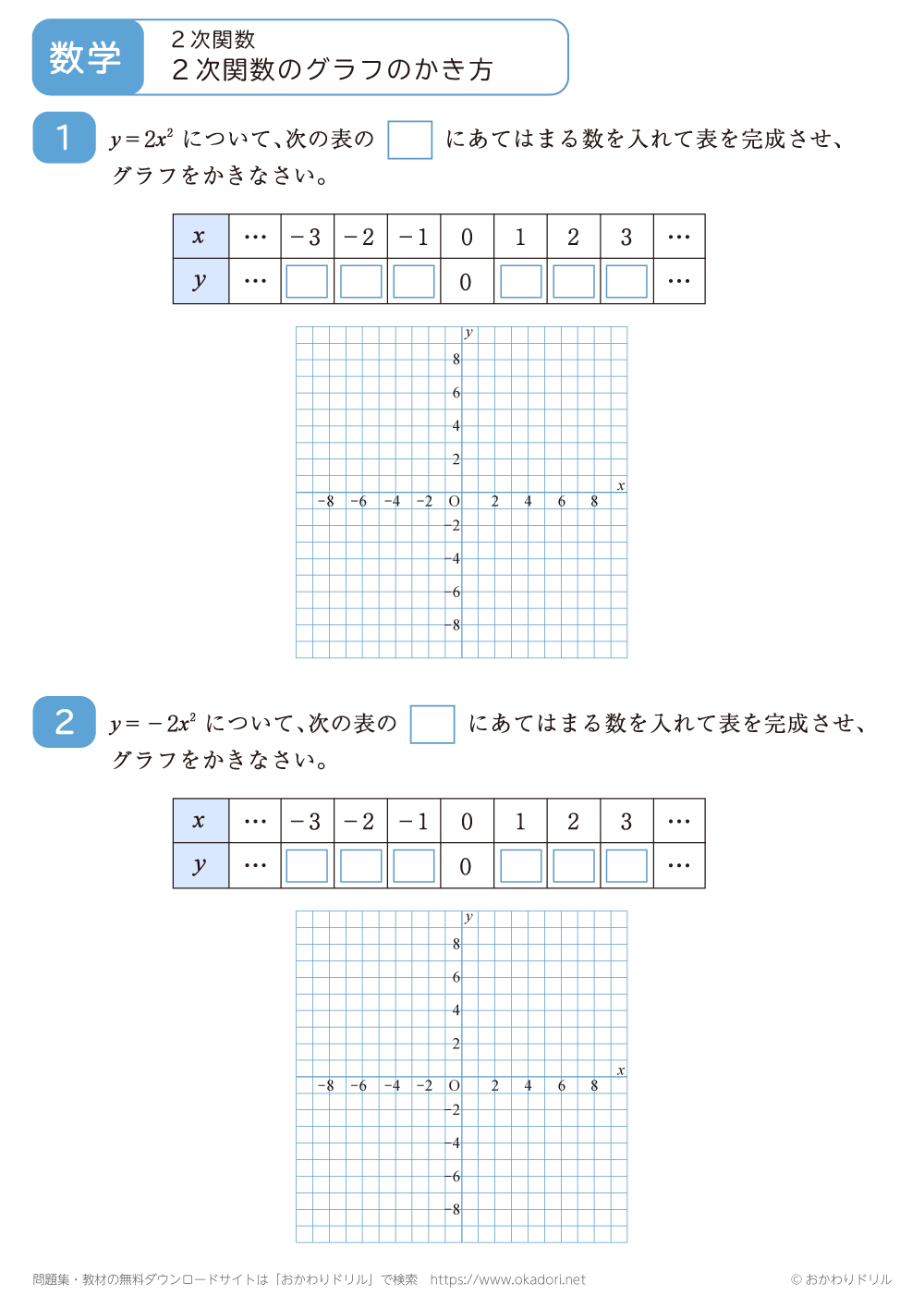
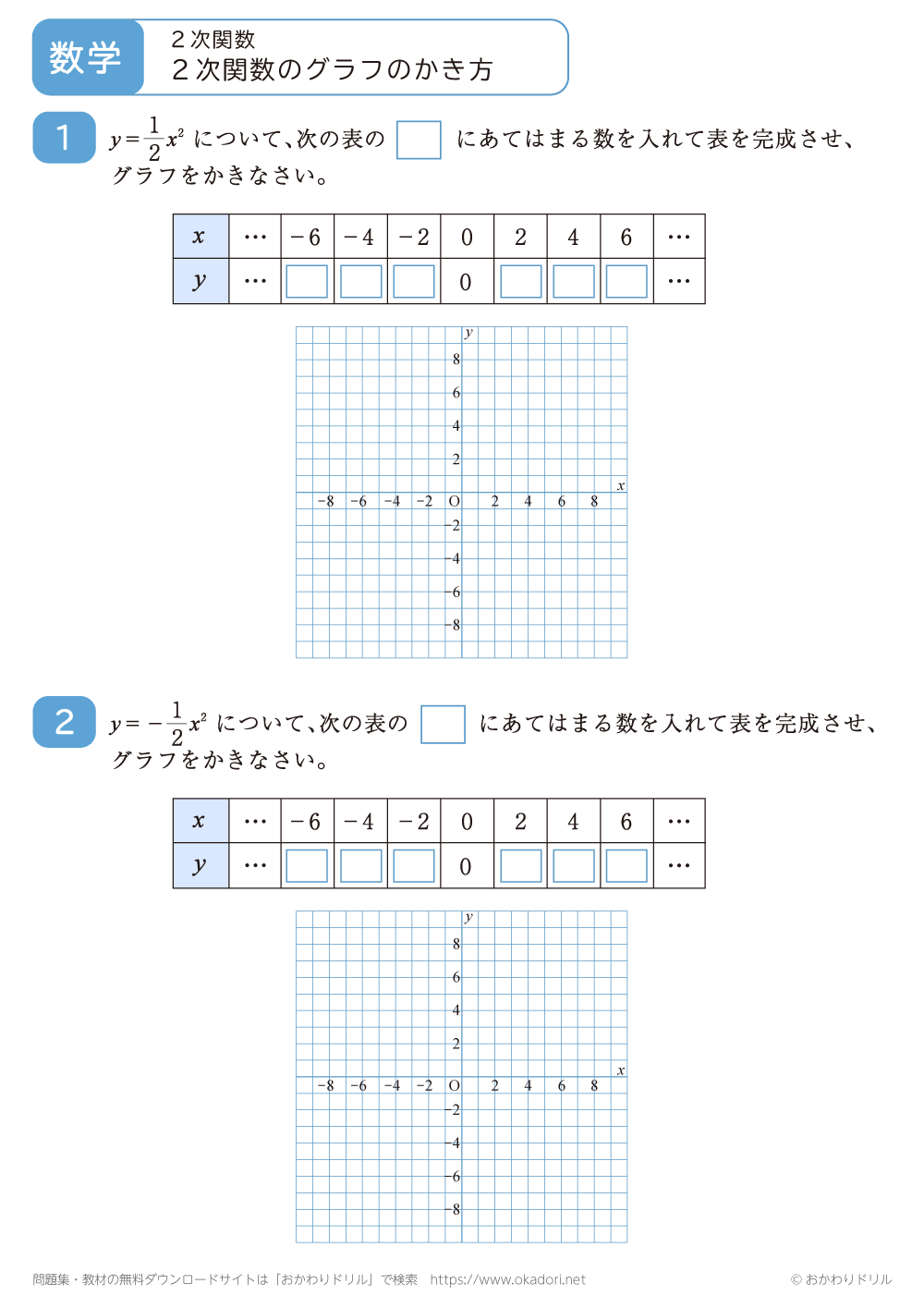
・関数y=ax2のグラフは、対応するx,yの値の組を座標とする点をいくつかとり、それらの点をなめらかな曲線で結びます。
・関数y=ax2のグラフには、次のような特徴があります。
1.原点を通り、y軸について対象な曲線となります。
2.a>0のときは、上に開く曲線となります。
3.a<0のときは、下に開く曲線となります。
4.aの絶対値が大きいほど、曲線はy軸に近づき、開き方は小さくなります。
5.aの絶対値が等しく、符号が異なる2つの曲線は、x軸について対称となります。

ぴよ校長
2次関数のグラフをかく問題を解いてみよう!
2次関数のグラフをかく問題です。関数y=ax2のaの値がいろいろなときに、どのようなグラフになるか考えながら問題を解いてみましょう。

ぴよ校長
それでは、さっそく問題を解いてみよう!
「2次関数のグラフのかき方」の学習プリントはこちら
下の画像やリンク文字をクリックするとのPDFファイルが開きます。ダウンロード・印刷してご利用ください。
解説テキスト
問題プリント
「2次関数」の問題プリント一覧