このページは、中学3年生で習う「２次関数の値の変化・変域・変化の割合」が学習できるページです。
この問題のポイント
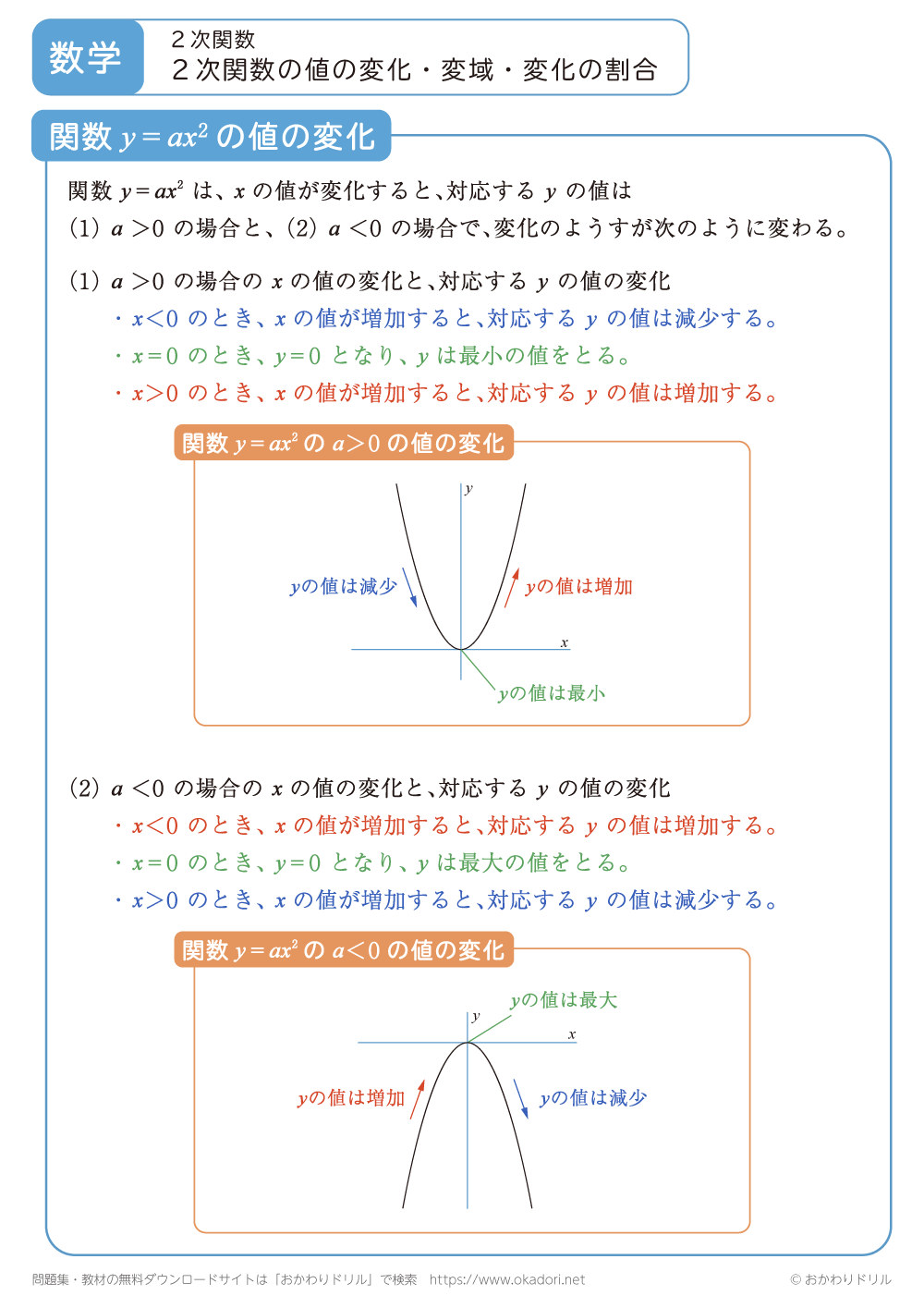
・関数ｙ＝ａｘ2は、ｘの値が変化すると、対応するｙの値は（１）ａ＞０の場合、（２）ａ＜０の場合で変化のようすが次のように変わります。
（１）ａ＞０の場合
ｘ＜０のときｘの値が増加するにつれｙの値は減少し、ｘ＝０のときｙ＝０となりｙは最小の値をとる。ｘ＞０のときｘの値が増加するにつれｙの値は増加する。
（２）ａ＜０の場合
ｘ＜０のときｘの値が増加するにつれｙの値は増加し、ｘ＝０のときｙ＝０となりｙは最大の値をとる。ｘ＞０のときｘの値が増加するにつれｙの値は減少する。
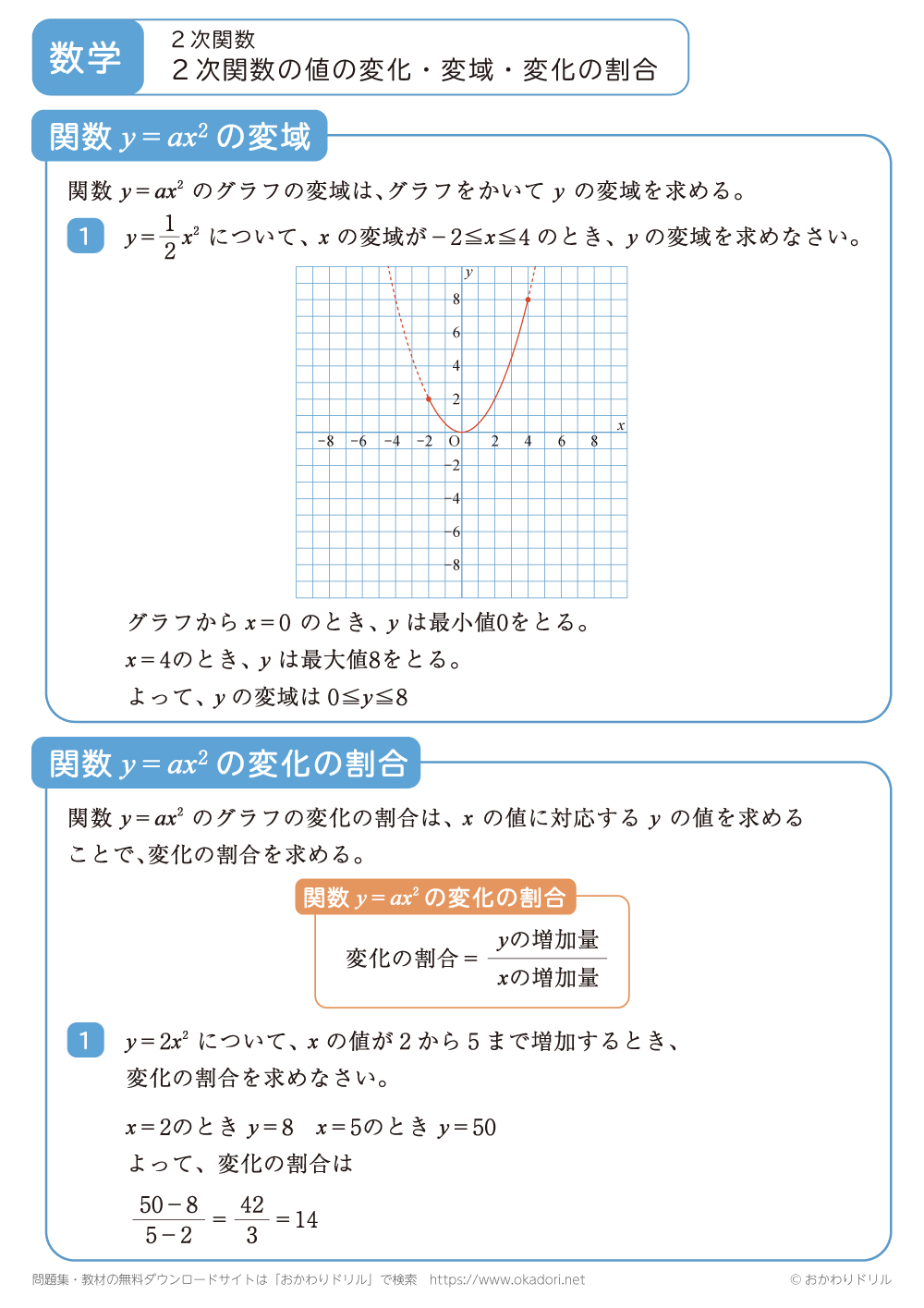
・関数ｙ＝ａｘ2の変域を求めるときは、グラフをかいてｙの変域を求めます。
・関数ｙ＝ａｘ2の変化の割合は、ｘの値に対応するｙの値を求めることで、変化の割合を求めます。
変化の割合＝（ｙの増加量）／（ｘの増加量）
ぴよ校長
２次関数の値の変化、変域、変化の割合の問題を解いてみよう！
２次関数の値の変化、変域、変化の割合の問題です。関数ｙ＝ａｘ2のグラフをかいて、ｘの値に対応するｙの値を求めながら、変域や変化の割合を求めてみましょう。
ぴよ校長
それでは、さっそく問題を解いてみよう！
「２次関数の値の変化・変域・変化の割合」の学習プリントはこちら
下の画像やリンク文字をクリックするとのPDFファイルが開きます。ダウンロード・印刷してご利用ください。
解説テキスト
問題プリント
「２次関数」の問題プリント一覧